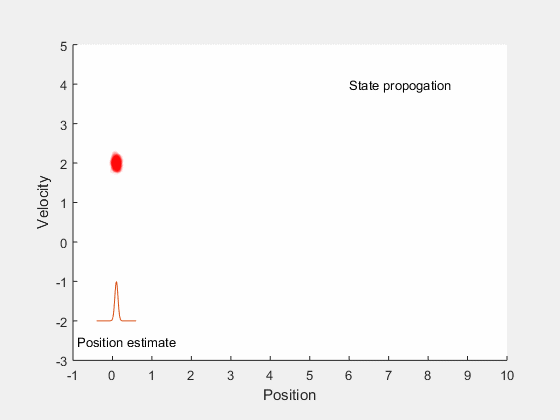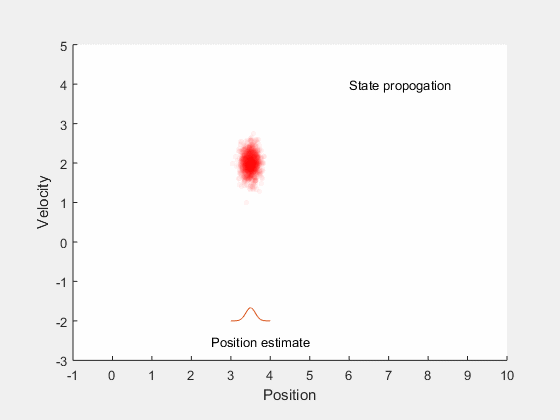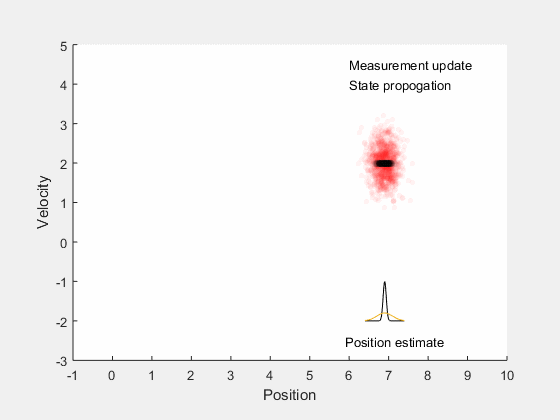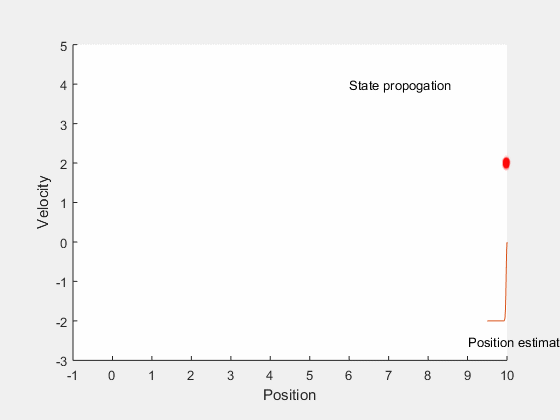
Kalman filter: Main idea¶
- Estimate future states based on system dynamics
- Update state estimates after getting measurement
- Find gain that minimizes error between true expected state and estimated state.
Discrete Kalman filter: Derivation¶
System dynamics
$$ X_{k+1} = AX_{k} + Bu_{k} + Fw_{k} $$\( w_k \) is uncertainity in the system dynamics and is represented as a Gaussian process, with covariance \( E(w_k w_k^T ) = Q \).
State variables \( X_k \) are also modeled as mutually independent Gaussian processes with covariance \( P_k \)
Initial conditions are now given as, \(X(0) = X_0 \) and covariance \( P_0 \).
Measurement¶
$$ Y_k = CX_k + Du_k + v_k $$- \( v_k \) is uncertainity in the measurement with covariance \( E(v_k v_k^T ) = R \).
System dynamics¶
$$ X_{k+1} = AX_{k} + Bu_{k} + Fw_{k} $$- \( E(w_k w_k^T ) = Q \), covariance \( P_k \), \(X(0) = X_0 \) and covariance \( P_0 \).
Measurement¶
$$ Y_k = CX_k + Du_k + v_k $$- \( v_k \) is uncertainity in the measurement with covariance \( E(v_k v_k^T ) = R \).
By repeating the process of measurement and state propogation successively, states can be estimates.
Notations¶
- \( X_{k|k} \) State estimate after measurement update
- \( X_{k+1|k} \) State estimate using system dynamics from \( k \) to \( k + 1 \).
- \( \bar{X} \) represents expected value of \( X \).
1. State propogation¶
System dynamics are given by,
$$ X_{k+1} = AX_{k} + Bu_{k} + F w_{k} $$To separate the state estimates before and after measurement, we define, \( X_{k|k} \) as estimate after measurement at step \( k \).
\( X_{k+1|k} \) is the state estimate after following system dynamics. Therefore the expected future value of the state are given by,
$$ E(X_{k+1|k} ) = AE(X_{k|k} ) + BE(u_k) + E(F w_k) $$$$ \hat{X}_{k+1|k} = A\hat{X}_{k|k} + B u_k $$The error between state estimate and expected value, before getting measurement is represented as,
$$ X_{k+1|k} - \bar{X}_{k+1|k} = AX_{k|k} + Bu_k + F w_k -( A\bar{X}_{k|k} + Bu_k ) $$$$ e_{k+1|k} = X_{k+1|k} - \bar{X}_{k+1|k} = Ae_{k|k} + F w_k$$Therefore, the covariance of state before getting measurement is given by,
$$ P_{k+1|k} = E(e_{k+1|k} e_{k+1|k}^{-T}) = P( (X_{k+1|k}- \bar{X}_{k+1|k})(X_{k+1|k} - \bar{X}_{k+1|k})^T) $$$$ P_{k+1|k} = A E(e_{k|k} e_{k|k}^T) A^T + E(Fw_k w_k^TF^T)$$Therefore, the error covariance propogation is given by,
$$ P_{k+1|k} = A P_{k|k} A^T + FQF^T . $$2. Update¶
Update covariance of state estimates after getting the measurement. The measurement are given by,
$$ Y_{k+1} = CX_{k+1|k} + Du_{k+1} + v_{k+1} $$The expected value of measurement is given by,
$$ \hat{Y}_{k+1} = C \hat{X}_{k+1|k}+ Du_{k+1} . $$
The error between state estimate and mean is given by,
$$ Y_{k+1} - \hat{Y}_{k+1}= CX_{k+1|k} + Du_{k+1} + v_{k+1} - ( C \hat{X}_{k+1|k} + Du_{k+1})$$$$ e_{Y,k+1} = Ce_{k+1|k} + v_{k+1} $$The covariance of measurement error before getting measurement is given by,
$$ E(e_{Y,k+1} e_{Y,k+1}^T) = E((Ce_{k+1|k} + v_{k+1})(Ce_{k+1|k} + v_{k+1})^T) $$$$ E(e_{Y,k+1} e_{Y,k+1}^T) = E((Ce_{k+1|k} + v_{k+1})(e_{k+1|k}^TC^T + v_{k+1}^T)) $$$$ = CP_{k+1|k}C^T + R $$- State update after measurement (same as observer update),
Choose a gain so the error between posterior state estimate and actual state is minimum.
$$ X_{k+1}- \hat{X}_{k+1|k+1} = X_{k+1}- \hat{X}_{k+1|k} - K_{k+1}C e_{k+1|k} -K_{k+1}v_{k+1} $$$$ e_{k+1|k+1} = (I - K_{k+1}C) e_{k+1|k} - K_{k+1} v_{k+1} $$The posterior error covariance becomes
$$ P_{k+1|k+1} = E( e_{k+1|k+1} e_{k+1|k+1}^T ) $$$$= E \left( ( (I - K_{k+1}C) e_{k+1|k} - K_{k+1} v_{k+1} ) ( (I - K_{k+1}C) e_{k+1|k} - K_{k+1}v_{k+1} ) ^T \right)$$$$= (I - K_{k+1}C) E (e_{k+1|k} e_{k+1|k}^T) (I - K_{k+1}C)^T + K_{k+1} E(v_{k+1} v_{k+1}^T) K_{k+1}^T$$$$P_{k+1|k+1} = (I - K_{k+1}C) P_{k+1|k} (I - K_{k+1}C)^T + K_{k+1}R K_{k+1}^T$$$$P_{k+1|k+1} = (I - K_{k+1}C) P_{k+1|k} (I - K_{k+1}C)^T + K_{k+1} R K_{k+1}^T$$$$P_{k+1|k+1} = P_{k+1|k} - K_{k+1}C P_{k+1|k} - P_{k+1|k} C^T K_{k+1}^T + K_{k+1} (C P_{k+1|k} C^T + R) K_{k+1}^T $$The trace of covariance matrix is the error between state estimate and update from measurement, therefore, the gain matrix that minimizes the covariance matrix is the optimal solution.
$$ \frac{\partial tr(P_{k+1|k+1} )}{\partial K_{k+1} } = -2 (CP_{k+1|k})^T + 2K_{k+1} (C P_{k+1|k} C^T + R) = 0$$Therefore,
$$ K_{k+1} = P_{k+1|k}C^T(C P_{k+1|k} C^T + R)^{-1} $$Substituting \( K_{k+1} \) in expression for posterior covariance gives,
$$P_{k+1|k+1} = P_{k+1|k} - K_{k+1}C P_{k+1|k} = ( I - K_{k+1}C ) P_{k+1|k} $$Final form of Kalman filter¶
1. State propogation¶
$$ \bar{X}_{k+1|k} = A\bar{X}_{k|k} + Bu_k $$$$ P_{k+1|k} = A P_{k|k} A^T + FQF^T . $$2. Measurement update¶
$$ e_{Y,k+1} = y(k+1) - ( C \hat{X}_{k+1|k} + Du_{k+1})$$$$ S_{k+1} = (C P_{k+1|k} C^T + R) $$$$ K_{k+1} = P_{k+1|k} C^TS_{k+1}^{-1}$$$$ \hat{X}_{k+1|k+1} = \hat{X}_{k+1|k} + K_{k+1}e_{Y,k+1}$$$$P_{k+1|k+1} = ( I - K_{k+1}C ) P_{k+1|k} $$Kalman filter: Example 1¶
Consider the system give
$$ \ddot{X} = u $$with measurement \( y = X \). We wish to develop an observer such that the states of the observer \( \hat{X} \rightarrow X \).
We approximate this system as follows,
$$ X_1(t+1) = X_1(t) + \delta t X_2 $$$$ X_2(t+1) = \delta t u $$The measurement is approximated as
$$ y = X + v $$where \( v \) is a Gaussian process with mean 0, and variance \( 10^{-8} \). Note as the system is determinitistic, we use a very low value of measurement covariance \( R \). As we know the system completely, we have \( F = [0~0]^T \).
clc
close all
clear all
A = [0 1 ; 0 0];
B = [0 ; 1];
dt = 0.001;
Ad = eye(2) + dt*[0 1 ; 0 0];
Bd = dt*B;
C = [1 0];
R = 1e-8;
F = [0;0];
Q = 0;
P_pl = eye(2);
X_hat_0 = [0;0];
X_0 = [1;0];
X(:,1)= X_0;
Y(1) = C*X(:,1);
t(1) = 0;
X_hat(:,1)= X_hat_0;
for i = 1:2000
u = 1;
t(i+1) = t(i)+dt;
% True process
X(:,i+1)=Ad * X(:,i) + Bd*u;
Y(i+1) = C*X(:,i+1)+sqrt(R)*randn;
P_mi = Ad*P_pl*Ad' + F*Q*F';
X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
Y_hat(i+1) = C*X_hat(:,i+1);
e_Y = Y(i+1) - Y_hat(i+1);
S = C*P_mi*C'+R;
K = P_mi*C'*inv(S);
P_pl = (eye(2) - K*C)*P_mi;
X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:),'--')
xlabel('time')
ylabel('Position')
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:),'--')
xlabel('time')
ylabel('Velocity')
Kalman filter: Example 2, noisy measurement, position measurement only¶
Consider the system give
$$ \ddot{X} = u $$with measurement \( y = X \). We wish to develop an observer such that the states of the observer \( \hat{X} \rightarrow X \).
We approximate this system as follows,
$$ X_1(t+1) = X_1(t) + \delta t X_2 $$$$ X_2(t+1) = \delta t u $$The measurement is approximated as
$$ y = X + v $$where \( v \) is a Gaussian process with mean 0, and variance \( 1 \).
clc
close all
clear all
A = [0 1 ; 0 0];
B = [0 ; 1];
dt = 0.001;
Ad = eye(2) + dt*[0 1 ; 0 0];
Bd = dt*B;
F = [0;0];
C = [1 0];
R = 1;
Q = 0;
P_pl = eye(2);
X_hat_0 = [0;0];
X_0 = [1;0];
X(:,1)= X_0;
Y(1) = C*X(:,1);
t(1) = 0;
X_hat(:,1)= X_hat_0;
for i = 1:5000
u = .5;
t(i+1) = t(i)+dt;
% True process
X(:,i+1)=Ad * X(:,i) + Bd*u;
Y(i+1) = C*X(:,i+1) + sqrt(R)*randn(size(C,1),1);
P_mi = Ad*P_pl*Ad' + F*Q*F';
X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
Y_hat(i+1) = C*X_hat(:,i+1);
e_Y = Y(i+1) - Y_hat(i+1);
S = C*P_mi*C'+R;
K = P_mi*C'*inv(S);
P_pl = (eye(2) - K*C)*P_mi;
X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:),'--')
xlabel('time')
ylabel('Position')
axis([0 5 0 10])
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:),'--')
xlabel('time')
ylabel('Velocity')
axis([0 5 -5 5])
Kalman filter: Example 3, noisy measurement, position and velocity measurements¶
Consider the system give
$$ \ddot{X} = u $$with measurement \( y = X \). We wish to develop an observer such that the states of the observer \( \hat{X} \rightarrow X \).
We approximate this system as follows,
$$ X_1(t+1) = X_1(t) + \delta t X_2 $$$$ X_2(t+1) = \delta t u $$The measurement is approximated as
$$ y_1 = X + v_1 $$$$ y_2 = \dot{X} + v_2 $$where \( v \) is a Gaussian process with mean 0, and identity variance.
clc
close all
clear all
A = [0 1 ; 0 0];
B = [0 ; 1];
dt = 0.001;
Ad = eye(2) + dt*[0 1 ; 0 0];
Bd = dt*B;
C = [1 0;
0 1];
F = [0;0];
R = diag([1 1]);
Q = 0;
P_pl = eye(2);
X_hat_0 = [0;0];
X_0 = [1;0];
X(:,1)= X_0;
Y(:,1) = C*X(:,1);
t(1) = 0;
X_hat(:,1)= X_hat_0;
for i = 1:5000
u = .5;
t(i+1) = t(i)+dt;
% True process
X(:,i+1)=Ad * X(:,i) + Bd*u;
Y(:,i+1) = C*X(:,i+1) + sqrt(R)*randn(size(C,1),1);
P_mi = Ad*P_pl*Ad' + F*Q*F';
X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
Y_hat(:,i+1) = C*X_hat(:,i+1);
e_Y = Y(:,i+1) - Y_hat(:,i+1);
S = C*P_mi*C'+R;
K = P_mi*C'*inv(S);
P_pl = (eye(2) - K*C)*P_mi;
X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:),'--')
xlabel('time')
ylabel('Position')
axis([0 5 0 10])
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:),'--')
xlabel('time')
ylabel('Velocity')
axis([0 5 -5 5])
Kalman filter for parameter estimation: Example 4 (position measurement only)¶
Consider the dynamic system given by,
$$ \dot{X_1} = X_2 + \alpha $$$$ \dot{X_2} = u $$\( \alpha \) is unknown.
$$ X_1(t+1) = X_1(t) + \delta t X_2 + \delta t X_3 $$$$ X_2(t+1) = \delta t u $$$$ X_3(t+1) = X_3(t) + w(t) $$where \( w(t) \) is a Gaussian process with covariance \( 10^{-4} \).
clc
close all
clear all
A = [0 1 1; 0 0 0;0 0 0];
B = [0 ; 1;0];
dt = 0.001;
Ad = eye(3) + dt*A;
Bd = dt*B;
F = [0;0;1];
C = [1 0 0];
R = .1;
Q = diag([1e-4]);
P_pl = eye(3);
X_hat_0 = [0;0;0];
X_0 = [1;0;10];
X(:,1)= X_0;
Y(:,1) = C*X(:,1);
t(1) = 0;
X_hat(:,1)= X_hat_0;
for i_sim = 1:5
A_sim(i_sim) = X_hat(3,1);
for i = 1:2500
u = .5;
t(i+1) = t(i)+dt;
% True process
X(:,i+1)=Ad * X(:,i) + Bd*u;
Y(:,i+1) = C*X(:,i+1) + sqrt(R)*randn(1,1);
% Observer model
% Prediction based on system dynamics
P_mi = Ad*P_pl*Ad' + F*Q*F';
X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
Y_hat(:,i+1) = C*X_hat(:,i+1);
% Update based on measurement
e_Y = Y(:,i+1) - Y_hat(:,i+1);
S = C*P_mi*C'+R;
K = P_mi*C'*inv(S);
P_pl = (eye(3) - K*C)*P_mi;
X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
end
X_hat(3,1) = X_hat(3,end);
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:),'--')
axis([0 2.5 0 40])
xlabel('time')
ylabel('Position')
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:),'--')
xlabel('time')
ylabel('Velocity')
axis([0 2.5 0 2])
figure;
plot(t,X(3,:),t,X_hat(3,:),'--')
axis([0 2.5 0 12.5])
Kalman filter for parameter estimation: Example 5 (position and velocity measurement)¶
Kalman filters can be used for parameter estimation also. Consider the dynamic system given by,
$$ \dot{X_1} = X_2 + \alpha $$$$ \dot{X_2} = u $$where \( \alpha \) is a parameter that is unknown. The measurements \( y_1 = X_1 + v_1\) and \( y_2 = X_2 + v_2\) are available, where \( v \)s are Gaussian processes with variances \( R_1 = .1 , R_2 = .1 \). We can apply Kalman filtering technique for estimating the unknown parameter.
$$ X_1(t+1) = X_1(t) + \delta t X_2 + \delta t X_3 $$$$ X_2(t+1) = \delta t u $$$$ X_3(t+1) = X_3(t) + w(t) $$clc
close all
clear all
A = [0 1 1; 0 0 0;0 0 0];
B = [0 ; 1;0];
dt = 0.001;
Ad = eye(3) + dt*A;
Bd = dt*B;
F = [0;0;1];
C = [1 0 0;
0 1 0];
R = diag([.1 .1]);
Q = diag([1e-4]);
P_pl = eye(3);
X_hat_0 = [0;0;0];
X_0 = [1;0;10];
X(:,1)= X_0;
Y(:,1) = C*X(:,1);
t(1) = 0;
X_hat(:,1)= X_hat_0;
for i_sim = 1:1
A_sim(i_sim) = X_hat(3,1);
for i = 1:2500
u = .5;
t(i+1) = t(i)+dt;
% True process
X(:,i+1)=Ad * X(:,i) + Bd*u;
Y(:,i+1) = C*X(:,i+1) + sqrt(R)*randn(2,1);
% Observer model
% Prediction based on system dynamics
P_mi = Ad*P_pl*Ad' + F*Q*F';
X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
Y_hat(:,i+1) = C*X_hat(:,i+1);
% Update based on measurement
e_Y = Y(:,i+1) - Y_hat(:,i+1);
S = C*P_mi*C'+R;
K = P_mi*C'*inv(S);
P_pl = (eye(3) - K*C)*P_mi;
X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
end
X_hat(3,1) = X_hat(3,end);
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:),'--')
axis([0 2.5 0 40])
xlabel('time')
ylabel('Position')
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:),'--')
xlabel('time')
ylabel('Velocity')
axis([0 2.5 0 2])
figure;
plot(t,X(3,:),t,X_hat(3,:),'--')
axis([0 2.5 0 12.5])
Kalman filter: Continuous system (Kalman-Bucy filter)¶
Consider the system dynamics given by,
$$ \dot{X} = AX + Bu + Fw $$where \( w \) is a Gaussian process with zero mean and covariance \( Q \), and measurement given by
$$ y = CX + Du + v $$The filter for state estimate consists of 2 differential equations,
$$ \dot{\hat{X}} = A \hat{X} + Bu + K ( y - C \hat{X}+ Du) $$ $$ \dot{P} = A P + PA^T + FQF^T - K R K^T$$ $$K = P C^T R^{-1}$$$$ \dot{P} = A P + PA^T + FQF^T - P C^T R CP $$- In continuous case, the measurement error's covariance and apriori covairance both are \( R \). Further, the observer gain calculations involve taking inverse of the covariance of noise \( R \) matrix.
- The sensor with lower covariance noise will contribute more to the update.
- In the special infitite-time case, the riccati equation becomes,
Kalman filter continuous time: Example 6 (two sensors)¶
Consider the system, \( \ddot{x} = u \), with measurement on position alone.
2 sensors to measure position,
- one sensor is very accurate (covariance = 0.01),
- the other is not accurate (covariance = 1).
clc
close all
clear all
A = [0 1;0 0];
B = [0; 1];
C = [1 0;
1 0];
t = 0:0.001:20;
dt = t(2) - t(1);
X(:,1) = [1;0];
y(:,1) = C*X;
R_k = diag([1 .01]);
Q_k = diag([1 1]);
P_k = care(A',C',Q_k,R_k);
K_k = P_k*C'*inv(R_k);
L = K_k;
K_k
X_hat(:,1) = [0;0];
y_hat(:,1) = C*X_hat;
for i = 2:length(t)
u = .5;
X(:,i) = X(:,i-1) +dt * (A*X(:,i-1) + B*u);
y(:,i) = C*X(:,i) + sqrt(R_k)*randn(size(C,1),1);
X_hat(:,i) = X_hat(:,i-1) +dt * (A*X_hat(:,i-1) + B*u +L *(y(:,i-1)-y_hat(:,i-1)));
y_hat(:,i) = C*X_hat(:,i) ;
end
K_k =
0.1090 10.8956
0.0995 9.9504
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:))
legend('Actual','Estimate')
xlabel('time')
ylabel('Position')
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:))
xlabel('time')
ylabel('Velocity')
Linear Quadratic Gaussian¶
Linear Quadratic Gaussian control is a control scheme that uses Linear Quadratic Regulator (LQR) for control and kalman filter (Linear Quadratic Estimation (LQE)) for estimation.
Separation principle allows to design controller and observer separately
clc
close all
clear all
A = [0 1;0 0];
B = [0; 1];
C = [1 0];
% Controller design
R = diag([1]);
Q = diag([1e-2 1e-2]);
M_a = rank(ctrb(A,B));
P = care(A,B,Q,R);
K_u = inv(R)*B'*P;
t = 0:0.001:20;
dt = t(2) - t(1);
X(:,1) = [1;0];
y(:,1) = C*X;
% Observer design
R_k = diag([1 ]);
Q_k = diag([1 1]);
P_k = care(A',C',Q_k,R_k);
K_k = P_k*C'*inv(R_k);
L = K_k;
X_hat(:,1) = [0;0];
y_hat(:,1) = C*X_hat;
for i = 2:length(t)
u = -K_u*X_hat(:,i-1);
X(:,i) = X(:,i-1) +dt * (A*X(:,i-1) + B*u);
y(:,i) = C*X(:,i) + sqrt(R_k)*randn(size(C,1),1);
X_hat(:,i) = X_hat(:,i-1) +dt * (A*X_hat(:,i-1) + B*u +L *(y(:,i-1)-y_hat(:,i-1)));
y_hat(:,i) = C*X_hat(:,i) ;
end
figure;
subplot(2,1,1)
plot(t,X(1,:),t,X_hat(1,:))
legend('Actual','Estimate')
xlabel('time')
ylabel('Position')
subplot(2,1,2)
plot(t,X(2,:),t,X_hat(2,:))
xlabel('time')
ylabel('Velocity')
Kalman filter: Conclusion¶
- Very powerful technique for optimal state estimation
- Extensions for nonlinear filters (extended kalman filter and unscented kalman filter)
- Particle filter (simulation based filters)