Motivation¶
- Sliding mode control can be applied to supress and remove the effect of bounded modeling errors.
- We did not account for the type of modeling error, and compensated for the effect of uncertainity by applying a large control that took out the effect of uncertainity.
- In adaptive control, we learn a mathematical form of uncertainity, and use that in control instead.
Motivating example¶
Consider the example of a pendumum with a drag term
$$ I\ddot{x} + b\dot{x}|\dot{x}| + mgl sin(x) = u $$Rewrite as,
$$ a_1 \ddot{x} + a_2 \dot{x}|\dot{x}| + a_3 sin(x) = u $$Design a control scheme, that will learn \(a_1\), \(a_2\) and \(a_3\) while trying to track \(x_d\).
Redefine the variable \( s \).
$$ s =\dot{\tilde{x}} + \lambda \tilde{x} = (\dot{x}- \dot{x}_d) + \lambda(x-x_d) = \dot{x} -\dot{x}_r$$where we define,
$$ \dot{x}_r =\dot{x}_d - \lambda(x-x_d) $$$$ \ddot{x}_r =\ddot{x}_d - \lambda(\dot{x}-\dot{x}_d) $$$$ \dot{s} = \ddot{x} - \ddot{x}_r $$We will now define a Lyapunov function,
$$ L = \frac{1}{2} I s^2 $$Taking derivative, we get
$$ \dot{L} = s I \dot{s} = sI (\ddot{x} - \ddot{x}_r) $$Substituting, \( I \ddot{x} \) from true dynamic gives,
$$ \dot{L} = s (u - I\ddot{x}_r - b\dot{x}|\dot{x}| - mgl sin(x) ) $$As the parameters are not known, we need to estimate them. We can write, \( I\ddot{x}_r + b\dot{x}|\dot{x}| + mgl sin(x) \) as \( Y a \) where,
$$ Y = [\ddot{x}_r ~\dot{x}|\dot{x}|~ sin(x) ] $$and
$$ a = \left[ \begin{array}{c} I \\ b \\ mgl \end{array} \right] = \left[ \begin{array}{c} a_1 \\ a_2 \\ a_3\end{array} \right] $$Therefore,
$$ \dot{L} = s (u - Ya ) $$as \( a \) is not known, we use estimate of \( a\) in control. Therefore, \( u = Y\hat{a} - ks \).
$$ \dot{L} = s (Y\hat{a} - ks - Ya ) = -ks^2 + sY(\hat{a}-a) $$$$ \dot{L} = -ks^2 + sY\tilde{a} $$In the derivative of the Lyapunov function above, we have additional \( sY\tilde{a}\) term. If we can add a term to the original Lyapunov function so \( sY\tilde{a} \) gets canceled out, we are guaranteed performance for \( x \rightarrow x_d \).
We append the Lyapunov as follows,
$$ L = \frac{1}{2} I s^2 + \frac{1}{2} \tilde{a}^T P^{-1} \tilde{a} $$Taking derivative gives,
$$ \dot{L} = -ks^2 +sY\tilde{a} + \dot{\tilde{a}}^T P^{-1} \tilde{a} $$Where \( P \) is a diagonal matrix and represents adaptation rate. If we chose
$$ \dot{\tilde{a}}^T = sYP $$The derivative of the Lyapunov function changes as,
$$ \dot{L} = -ks^2 + sY\tilde{a} + sY \tilde{a} = -ks^2$$Therefore,
$$ \dot{\tilde{a}}^T = -sYP $$drives Lyapunov to zero. Further as Lyapunov is zero only when \( s = 0\) and \( a = \hat{a} \), we get \( \hat{a} \rightarrow a\).
$$ \dot{\tilde{a}}^T = \dot{\hat{a}}^T = -sYP $$Therefore, the adaptation law
$$ \dot{\hat{a}} = -P^TY^T s = -P Y^T s $$along with the control law,
$$ u = Y\hat{a} - ks $$gives \( x \rightarrow x_d \) and \( \hat{a} \rightarrow a \).
Important¶
The adaptation is a need-based, i.e. parameter estimation is based on tracking error, therefore, if tracking error is zero always, then parameters will not be updated. It can be shown that the sufficient condition for parameters to converge to the true parameters is
$$ I = \frac{1}{T} \int_t^{t+T} \tilde{a} Y_d^T Y_d a dt $$is a full rank matrix, over some intermediate interval \(T\).
Example: Nonlinear spring mass damper¶
For the system given by,
$$ 2\ddot{x} + \dot{x}|\dot{x}| + sin(x) = u $$design a control to track \( X_d = sin(t) \). Assume that none of the model parameters are known.
Solution:¶
We will choose our control \( u \) as
$$ u = Y\hat{a} - ks $$where
$$ Y = [\ddot{x}_r ~\dot{x}|\dot{x}|~ sin(x) ] $$and
$$ \ddot{x}_r =\ddot{x}_d - \lambda(\dot{x}-\dot{x}_d) . $$With parameter update rule,
$$ \dot{\hat{a}} = -P Y^T s $$In this example, the tracking error goes to zero, however, the parameters may not be fully estimated.
clc
close all
clear all
I = 2;
mgl = 1;
b = 1;
a = 0.5*[1;1;1];
lambda = 2;
p = 0.5*eye(1);
k = 1;
dt = 0.001;
t(1) = 0;
X(:,1) = [0;1];
for i = 2:50000,
t(i) = t(i-1)+dt;
ddX_r = -sin(t(i)) - lambda*(X(2,i-1) - cos(t(i)));
Y = [ddX_r X(2,i-1)*abs(X(2,i-1)) sin(X(1,i-1))];
s = (X(2,i-1) - cos(t(i))) + lambda*(X(1,i-1) - sin(t(i)));
a = a - p*Y'*s*dt;
a_all(:,i) = a;
u = Y*a - k*s;
X(1,i) = X(1,i-1) + dt * X(2,i-1);
X(2,i) = X(2,i-1) + dt * ( u - b*abs(X(2,i-1))*X(2,i-1) - mgl*sin(X(1,i-1)) )/I;
end
plot(t,X(1,:),t,sin(t))
xlabel('time')
ylabel('X')
Neural networks based control¶
- Adaptive control requires accurate knowledge of the system
- Structure of function not known
- Neural networks are very good approximators
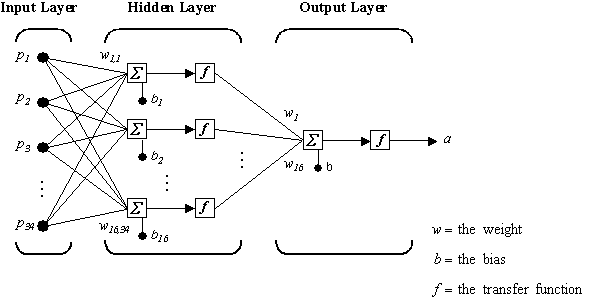
Linear in parameter neual network (LPNN) control:¶
- Simplest neural network is Linear in Parameter Neural Network, LPNN.
- Based on the idea of kernel trick
- Express unknown as a linear function of nonlinear functions (similar to fourier series, but more generalizable).
LPNN:¶
Consider a system given by,
$$ \dot{X} = f(X) + g(X) u + D(x) $$where \( D \) is some unmodeled dynamics.
- \( \phi \) represents a vector of basis functions,
- \( \epsilon \) is approximation error and can be made as small as possible.
Choose a control \( u \) and a weight update scheme such that
- \( X \rightarrow 0 \) and
- \( W \rightarrow W_{ideal} \)
We first define an approximate system,
$$ \dot{X}_a = f(X) + g(X) u + W^T \phi(X) + K (X - X_a) $$We define error between \( e = X-X_a \) as,
$$ \dot{e} = D(x) - W^T \phi(X) - K (X - X_a) = \tilde{W}^T \phi(X) - K e + \epsilon $$where, \( \tilde{W} = W_{ideal} - W \).
We now define a Lyapunov,
$$ L = \frac{1}{2} e^Te + \frac{1}{2} trace(\tilde{W}^T P^{-1}\tilde{W} )$$Taking derivative gives,
$$ \dot{L} = e^T\dot{e} + trace(\tilde{W}^T P^{-1}\dot{\tilde{W}} )$$Taking derivative and rearranging terms gives,
$$\dot{L} = e^T (\tilde{W}^T \phi(X) - K e + \epsilon) + trace(\tilde{W}^T P^{-1}\dot{\tilde{W}} )$$ $$\dot{L} = e^T \tilde{W}^T \phi(X) - e^T K e + e^T\epsilon + trace(\tilde{W}^T P^{-1}\dot{\tilde{W}} )$$ $$\dot{L} = trace( \tilde{W}^T \phi(X)e^T) - e^T K e + e^T\epsilon + trace(\tilde{W}^T P^{-1}\dot{\tilde{W}} )$$ $$\dot{L} = - e^T K e + e^T\epsilon + trace(\tilde{W}^T P^{-1}\dot{\tilde{W}} + \tilde{W}^T \phi(X)e^T)$$ $$\dot{L} = - e^T K e + e^T\epsilon + trace(\tilde{W}^T (P^{-1}\dot{\tilde{W}} +\phi(X)e^T))$$and get,
$$\dot{L} = - e^TK e + e^T\epsilon $$$$\dot{L} = - e^TK (e - K^{-1}\epsilon) $$LPNN control¶
$$ \dot{W} = P\phi(X)e^T $$ $$ u = v-g(x)^{-1}W^T\phi(X) $$Note, \( e \) is the error between true system and approximate system,
$$ \dot{X}_a = f(X) + g(X) u + W^T \phi(X) + K (X - X_a) $$Regularization:¶
In practice we choose the weights as,
$$ \dot{W} = P\phi(X)e^T - \delta |e|W $$which penalaizes large \( W \) and acts as a regularization term. Regularization prevents overfitting the data, and results in a model that accounts for all the features in data. \( \delta \) is typically chosen as a small number, so the regulairzation kicks in only when the weights become very large.
Example:¶
Consider a simple system given by
$$ \dot{X} = u $$Say we fail to model the complex dynamics, \( \alpha + sin(2X) \), and approximate it as a sin fourier series with 16 terms.
clc
close all
clear all
dt = 0.001;
P = 0.01;
alp = 2;
X(1) = 1;
X_a(1) = 1;
t(1) = 0;
K = 50;
W(:,1) = 0*rand(16,1);
for i = 2:100000
t(i) = t(i-1) + dt;
D(:,i) = alp+sin(X(i-1));
phi_x = [1;sin(X(i-1));sin(2*X(i-1));sin(3*X(i-1));
sin(4*X(i-1));sin(5*X(i-1));sin(6*X(i-1));
sin(7*X(i-1));sin(8*X(i-1));sin(9*X(i-1));
sin(10*X(i-1));sin(11*X(i-1));sin(12*X(i-1));
sin(13*X(i-1));sin(14*X(i-1));sin(15*X(i-1));];
u = -W(:,i-1)'*phi_x + sin(.5*t(i-1)) - .1*X(i-1);
% True system
X(i) = X(i-1) + dt*( D(:,i) + u);
% Approximate system
X_a(i) = X_a(i-1) + dt*( W(:,i-1)'*phi_x + u + K*(X(i-1)-X_a(i-1)));
W(:,i) = W(:,i-1) + P*phi_x*(X(i)-X_a(i)) - .0001*abs(X(i)-X_a(i))*W(:,i-1);
D_approx(:,i) = W(:,i-1)'*phi_x ;
end
figure;
plot(t,X_a,t,X)
figure;
subplot(2,1,1)
plot(t,D,t,D_approx)
subplot(2,1,2)
plot(t,D-D_approx)
figure;
subplot(2,2,1)
plot(t,W(1,:))
ylabel('w_1')
xlabel('time')
subplot(2,2,2)
plot(t,W(2,:))
ylabel('w_2')
xlabel('time')
subplot(2,2,3)
plot(t,W(3,:))
ylabel('w_3')
xlabel('time')
subplot(2,2,4)
plot(t,W(4,:))
ylabel('w_4')
xlabel('time')