Motivation¶
- Express dynamics system as a cascade of systems.
- Start with the most difficult control fist, and go back and solve simpler control problems.
- Work with fewer simpler equation instead of one complex equation.
Backstepping: Example¶
Consider the system given by,
$$ \dot{y} = v $$and
$$ \ddot{z} + \dot{z}^3 - z^5 + yz = 0 $$The system has relative degree of 1, and the zero dynamics is given by,
$$Zero~dynamics:~ \ddot{z} + \dot{z}^3 - z^5 = 0 $$The zero dynamics above is not stable, and therefore, driving \( y \) to zero may result in the whole system becoming unstable.
However, say we could chose \( y \) as \(2 z^4 \), then the residual dynamics becomes
$$ \ddot{z} + \dot{z}^3 + z^5 = 0 $$which is stable.
Lyapunov?
How to choose control \( v \) ?
Choosing \(v = z \dot{z} + 8 z^3 \dot{z} + (2z^4 - y) \) gives,
$$ \dot{L} = -\dot{z}^4 - (2z^4 -y )^2 $$Example 2:¶
Given the system below, we want to drive \( x \rightarrow 0 \). Choose control law \( u \) such that \( x \rightarrow 0\) and \( y \) and \( z \) remain bounded.
$$ \dot{x} + x^2 y^5 z e^{xy} = (x^4 + 2 ) u $$ $$ \dot{y} + y^3 z^2 -x = 0 $$ $$ \ddot{z} + \dot{z}^3 - z^5 + yz = 0 $$we first perform a nonlinear transformation on control \( u \), and set,
$$ v = (x^4 + 2 ) u - x^2 y^5 z e^{xy} $$so the first system changes as,
$$ \dot{x} = v $$Further, if we define \( w = x - y^3z^2 \),
$$ \dot{y} = w $$ $$ \ddot{z} + \dot{z}^3 - z^5 + yz = 0 $$We will first work with lower 2 systems.
The last 2 equations are the same as Example 1, therefore, by choosing, \( w = z \dot{z} + 8 z^3 \dot{z} + (2z^4 - y) \) we can stabilize \( z \). Therefore, we want
$$ x = w+y^3 z^2 = z \dot{z} + 8 z^3 \dot{z} + (2z^4 - y) + y^3 z^2 = x_o $$Lyapunov:¶
$$ L = \frac{1}{6} z^6 + \frac{1}{2}\dot{z}^2 + \frac{1}{2}(y-2z^4)^2 + \frac{1}{2}(x-x_o)^2 $$Taking derivative gives,
$$\dot{L} = -\dot{z}^4 - (y-2z^4)^2 + (x-x_o)( \dot{x}- \dot{x}_o) = -\dot{z}^4 - (y-2z^4)^2 + (x-x_o)( v - \dot{x}_o) $$Note \( \dot{x}_o\) is a big algebraic expression in \(x,y,z,\dot{x},\dot{y},\dot{z}\), choose \( v = \dot{x}_o -(x-x_o) \), this gives the derivative of Lyapunov as,
$$\dot{L} = -\dot{z}^4 - (y-2z^4)^2 - (x-x_o)^2 $$Backstepping formal definition¶
Consider the system given by,
$$ \dot{ \eta} = f(\eta) + g(\eta) \zeta $$$$ \dot{ \zeta} = u $$where \( u \) is the control input. We can treat \( \zeta \) as a virtual control input for \(\dot{ \eta} = f(\eta) + g(\eta) \zeta \). Say \( \zeta = \phi(\eta) \) stabilizes the system. i.e. for
$$ L_o = \frac{1}{2} \eta^2 $$$$ \dot{L}_o = \eta \dot{\eta} = \eta(f(\eta) + g(\eta) \phi(\eta) )<0 $$We will now investigate the stability of the entire system by choosing a Lyapunov function,
$$ L = L_o + \frac{1}{2}(\zeta - \phi(\eta))^2 $$Taking the derivative gives,
$$ \dot{L} = \dot{L}_o + (\zeta - \phi(\eta))(\dot{\zeta} - \dot{\phi}(\eta)\dot{\eta}) = \dot{L}_o + (\zeta - \phi(\eta))(v - \dot{\phi}(\eta)(f(\eta) + g(\eta) \zeta)) $$Choosing, \( v = - (\zeta - \phi(\eta)) + \dot{\phi}(\eta)(f(\eta) - g(\eta) \zeta) \) gives,
$$ \dot{L} = \dot{L}_o - (\zeta - \phi(\eta))^2 < 0 $$The derivative of Lyapunov above is always decreasing and it is equal to zero when the
Backstepping method¶
Consider a system given by the equations below,
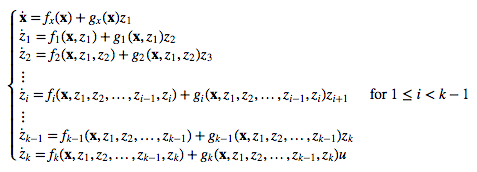
where \( z_i \) are scalar states, \( u \) is a scalar input, along with,
$$ g_{i}({\mathbf {x}},z_{1},\ldots ,z_{k})\neq 0 $$and
$$ f_i({\mathbf {x}}) = 0 $$for all \( i\).
Backstepping control can recursively be designed in the following steps,¶
1. Design a stabilizing control \( u_x(\mathbf{x})\)¶
$$ {\dot {{\mathbf {x}}}}=f_{x}({\mathbf {x}})+g_{x}({\mathbf {x}})u_{x}({\mathbf {x}})$$Say a control \( u_x\) exists that stabilizes the system above, further we assume that a Lyapunov \( L_x \) exists and is known.
2. Choose \( u_1 \) so \(z_1 \) follow \( u_x \).¶
$$ {\dot {z}}_{1}=f_{1}({\mathbf {x}},z_{1})+g_{1}({\mathbf {x}},z_{1})u_{1}({\mathbf {x}},z_{1}) $$To design \( u_1 \) we choose a Lyapunov,
$$ L_1 = L_x + \frac{1}{2}(z_1 - u_x(\mathbf{x}))^2 $$