Wheeled robot¶
- Backstepping control
- Kinematics, dynamics and motor control are separate dynamics tasks
Model of unicycle¶
Consider the wheeled robot shown below,
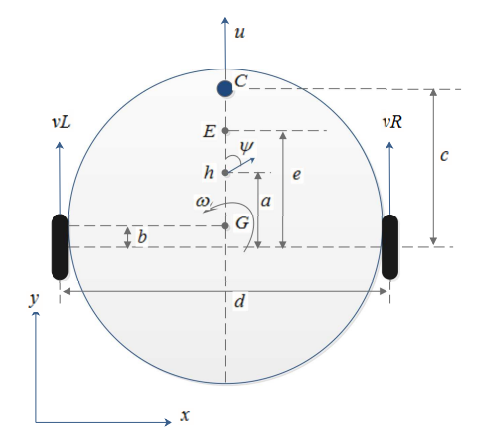
where,
- C is location of castor wheel
- G is location of the center of mass of the robot
- \( \psi \) is the robot orientation, \( x \) and \( y \) are locations of center of mass in XY-plane.
- \( u \) and \( \omega \) are linear and angular veloticies of the robot.
The full dynamic model of the robot can be written as,
$$ \left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\psi} \\ \dot{u} \\ \dot{\omega} \end{array} \right] = \left[ \begin{array}{c} u cos(\psi) - a \omega \sin(\psi) \\ u sin(\psi) + a \omega \cos(\psi) \\ \omega \\ \frac{\lambda_3}{\lambda_1} \omega^2 - \frac{\lambda_4}{\lambda_1} u \\ -\frac{\lambda_5}{\lambda_2} u \omega - \frac{\lambda_6}{\lambda_2} \omega \end{array} \right] + \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \frac{1}{\lambda_1} & 0 \\ 0 & \frac{1}{\lambda_2} \end{array} \right] \left[ \begin{array}{c} u_{ref} \\ \omega_{ref} \end{array} \right]$$Kinematics¶
$$ \dot{x} = u cos(\psi) - a\omega sin(\psi) = \mu_x$$$$ \dot{y} = u sin(\psi) + a\omega cos(\psi) = \mu_y $$$$ \dot{\psi} = \omega $$
$$ \left[ \begin{array}{cc} cos(\psi) & - a sin(\psi) \\ sin(\psi) & a cos(\psi) \end{array} \right] \left[\begin{array}{c} u \\ \omega \end{array} \right] = \left[\begin{array}{c} \mu_x \\ \mu_y \end{array} \right] $$
or
$$\left[\begin{array}{c} u \\ \omega \end{array} \right] = \left[ \begin{array}{cc} cos(\psi) & sin(\psi) \\ \frac{-1}{a} sin(\psi) & \frac{1}{a} cos(\psi) \end{array} \right] \left[\begin{array}{c} \mu_x \\ \mu_y \end{array} \right] $$Dynamics¶
$$ \dot{u} = \omega^2 - u + u_{ref}$$ $$ \dot{\omega} = u \omega - \omega + \omega_{ref}$$Backstepping inner loop:¶
$$ s = \tilde{q} = q - q_d $$where, \(q = [x~y~\psi] \) and \( q_d\) represents the desired trajectory.
We define a Lyapunov as,
$$ L = \frac{1}{2} \tilde{q}^T \tilde{q} $$Taking derivative gives,
$$ \dot{L} = \tilde{q}^T \dot{\tilde{q}} = \tilde{q}^T (\dot{q} - \dot{q}_d) $$ $$ \dot{L} = (x-x_d)\mu_x + (y-y_d) \mu_y + (\psi - \psi_d) \omega $$ $$ \dot{L} = (x-x_d)(\mu_x - \dot{x}_d) + (y-y_d) (\mu_y - \dot{y}_d) + (\psi - \psi_d)(\omega - \dot{\psi}_d) $$Therefore choosing,
$$ \mu_x = - K_x(x-x_d) + \dot{x_d} $$$$ \mu_y = - K_y(y-y_d) + \dot{y_d} $$$$ \omega = - K_\psi(\psi - \psi_d)+ \dot{\psi}_d $$Gives the Lyapunov function as,
$$ \dot{L} = - K_x(x-x_d)^2 - K_y (y-y_d)^2 -K_\psi (\psi - \psi_d)^2 $$Therefore,
$$ u = (- K_x(x-x_d) + \dot{x_d} ) cos(\psi) + (- K_y(y-y_d) + \dot{y_d}) sin(\psi) = u_d $$and
$$ \omega = -\frac{1}{a} \left( (- K_x(x-x_d) + \dot{x_d} ) sin(\psi) -(- K_y(y-y_d) + \dot{y_d}) cos(\psi)\right) = \omega_d $$
$$ L_u = \frac{1}{2} \tilde{q}^T \tilde{q} + \frac{1}{2}(u-u_d)^2 + \frac{1}{2}(\omega-\omega_d)^2 $$
Derivative of Lyapunov¶
$$ \dot{L}_u = \tilde{q}^T \dot{\tilde{q}} + (u-u_d)(\dot{u}-\dot{u}_d) + (\omega -\omega_d)(\dot{\omega}-\dot{\omega}_d) $$From before, we have,
$$ \dot{L}_u = (u-u_d)(\dot{u}-\dot{u}_d) + (\omega-\omega_d)(\dot{\omega}-\dot{\omega}_d) - K_x(x-x_d)^2 - K_y (y-y_d)^2 -K_\psi (\psi - \psi_d)^2 $$$$ \dot{L}_u = (u-u_d)(\dot{u}-\dot{u}_d) + (\omega-\omega_d)(\dot{\omega}-\dot{\omega}_d) - K_x(x-x_d)^2 - K_y (y-y_d)^2 -K_\psi (\psi - \psi_d)^2 $$Choosing,
$$ u_{ref}= -K_u(u-u_d) + \dot{u}_d + u - \omega^2 $$and
$$ \omega_{ref}= -K_\omega (\omega-\omega_d) + \dot{\omega}_d + \omega - u \omega $$gives,
$$ \dot{L}_u = -K_u(u-u_d)^2 + -K_\omega(\omega-\omega_d)^2- K_x(x-x_d)^2 - K_y (y-y_d)^2 -K_\psi (\psi - \psi_d)^2 $$Final backstepping control¶
Therefore,
$$ u_d = (- K_x(x-x_d) + \dot{x_d} ) cos(\psi) + (- K_y(y-y_d) + \dot{y_d}) sin(\psi) $$and
$$ \omega_d = -\frac{1}{a} \left( (- K_x(x-x_d) + \dot{x_d} ) sin(\psi) -(- K_y(y-y_d) + \dot{y_d}) cos(\psi)\right) $$along with,
$$ u_{ref}= -K_u(u-u_d) + \dot{u}_d + u - \omega^2 $$and
$$ \omega_{ref}= -K_\omega (\omega-\omega_d) + \dot{\omega}_d + \omega - u \omega $$gives a stable control system that drives states to desired values.
In [ ]: