Optimal control

Vivek Yadav, PhD

In previous classes, we saw how to use pole-placement technique to design controllers for regularization, set-point tracking, tracking time-dependent signals and how to incorporate actuator constraints into control design. Pole-placement technique involves obtaining a gain matrix such that the resulting system dynamics under the effect of control has poles at user-specified loaction. However, we did not look into how to best choose the poles of the system. Consider the example of a double integrator $ \ddot{x} = u $.

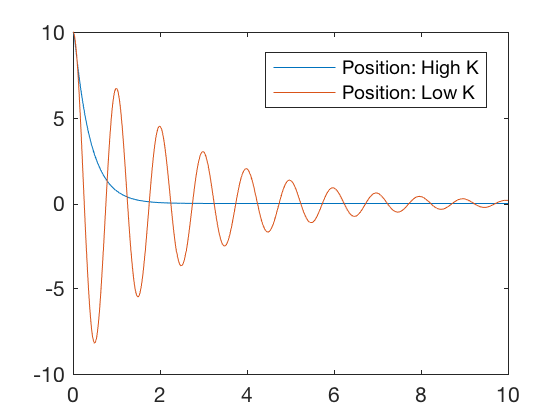
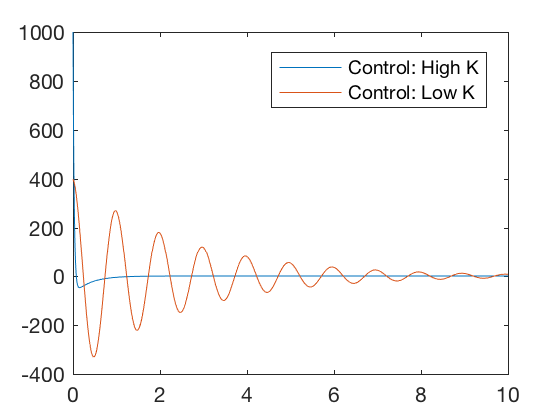
Consider two controllers characterized by a high and a low value of the gain matrix. Figures below illustrate that for high value of the gain matrix, the errors go to zero quickly, but the required control signal is very high. For a lower value of the gain matrix, the errors go to zero much slower but the required control signal is low. Therefore, by choosing the gain matrix appropriately, a control designer can choose an optimal point between the high and low gain values where the errors go to zero reasonably quickly for reasonable values of control signals. In this class, we will visit 3 different optimal control design techniques,

Linear quadratic regulator (LQR) control formulation (first variance principles)
Dynamic programming for LQR
- Path planning
- LQR using dynamic programming
Numerical methods for optimization
- Direct collocation/Direct transcription
- Bang-bang control
- Revisiting LQR control

clc
close all
clear all

K_high = [100 40];
K_low = [40 .8];
x0= [10;0];

t = 0:0.01:10;
K = K_high;
sys_fun = @(t,x)[x(2); -K*x];
[t X_high] = ode45(sys_fun,t,x0);
K = K_low;
sys_fun = @(t,x)[x(2); -K*x];
[t X_low] = ode45(sys_fun,t,x0);

figure;
plot(t,K_high*X_high',t,K_low*X_low')
legend('Control: High K','Control: Low K')
figure;
plot(t,X_high(:,1),t,X_low(:,1))
legend('Position: High K','Position: Low K')

Optimal control formulation

General case: NO time, path or control constraint.

We first deal with the most general case of optimal control, where there are no constraints on the path, control signal or time to completion. Consider the system given by,

$\dot{X} =f(x,u),$

with initial condition $ X(0) = X_0 $. We wish to find a control policy $ u $ that minimizes a cost of the form,

$J(u) = \Phi(X_f) + \int_{t=0}^{t_f} L(t,X,u) dt .$

The optimal control problem can now be formulated as,

$Minimize ~ J (u)$

Subject to,

$\dot{X} = f(X,u) \text{ and }$ $X(0) = X_0$

Deriving necessary conditions for optimization,

The first step in obtaining control law is to dervie the necessary conditions that the controller needs to satisfy. We do so by first appending the system dynamics equation to the integrand in the error function to get,

$J(u) = \Phi(X_f) + \int_{t=0}^{t_f} \left( L(t,X,u) + \lambda^T (f(x,u) - \dot{x} ) \right)dt .$

Defining a Hamiltonian $ H( x,u,\lambda ) $ as,

$H( x,u,\lambda) = L(t,X,u) + \lambda^T f(x,u),$

The optimal control problem can now be rewritten as,

$J(u) = \Phi(X_f) - \int_{t=0}^{t_f} \left( H( x,u,\lambda) - \lambda^T \dot{x} \right)dt .$

Using integration by parts on the second term in the integrant becomes

$\int_{t=0}^{t_f}\lambda^T \dot{x} dt = \lambda^T (X_f - X_0) - \int_{t=0}^{t_f} \dot{\lambda}^T x dt .$

Substituting it back in the integrand,

$J(u) = \Phi(X_f) - \lambda^T (X_f - X_0) + \int_{t=0}^{t_f} \left( H( x,u,\lambda) + \dot{\lambda}^T x \right)dt .$

We will next takes first variance in $ J $ introduced by a first variance $ \delta u $ in the control. As the states also depend on the control, a variation in control will result in variation in state, and this is represented as $ \delta x $. Taking first variance with respect to $ u $ gives,

$\delta J = \left. \left( \frac{\partial \Phi }{\partial X} - \lambda^T \right) \delta x \right|_{t_f,X_f} + \int_{t=0}^{t_f} \left[ \left( \frac{\partial H }{\partial X} + \dot{\lambda}^T \right) \delta x + \left( \frac{\partial H }{\partial u} \right) \delta u \right]dt .$

As $ \lambda (t) $ are arbitary, we can choose them to satisfy $ \delta J = 0 $ and for this choice of $ \lambda (t) $, we get an optimal solution. The conditions for optimality can be written as,

$\dot{\lambda}= - \frac{\partial H }{\partial X}^T ,$

with the final value condition

$\lambda_f = \left. \frac{\partial \Phi }{\partial X} ^T \right|_{t_f,X_f} .$

These equations in $ \lambda $ are also known as costate equations. The control is given by the stationary condition,

$\frac{\partial H }{\partial u} = 0$

And the evolution of states is given by,

$\dot{X} = f(X,u) \text{ and }$ $X(0) = X_0$

The state and co-state equation represent the necessary conditions that the optimal control law must satisfy. The boundary conditions on the state variables are defined at initial condition and the boundary conditions on co-state variables are defined at final time. Solving this two-point boundary value problem is very difficult, and several numerical methods are developed. We will look into a few of those methods later in the course. In special case where the system is linear, we can express the costate as a linear function of states and cost as a quadratic function of state and control, a general state-independent solution can be obtained.

Continuous time finite horizon, Linear quadratic regulator

For linear systems, we can get a state-independent representation of costate equation by expressing costate as a linear function of states and cost is a quadratic function of state and control. This form as Linear Quadratic Control (LQR). In LQR we choose controller to minimize a quadratic cost of states and control,

$J(u) =\frac{1}{2} X_f^T S X_f +\frac{1}{2} \int_{t=0}^{t_f} (X^TQX + u^T R u) dt .$

Where, $ Q $ is a semi-positive definite matrix representing the cost on state deviations from 0, $ R $ is a positive-definite matrix indicating the control cost, and $ S $ is a positive definite matrix penalizing the error from the final desired value of $ 0 $. $ Q $ and $ R $ are typically chosen as a diagonal matrix, and higher values of $ Q $ penalize trajectory error and high $ R $ penalizes control. Therefore, using this formulation reduces the job of control designer from identifying poles of the system, to setting relative weights of the control cost and trajectory error. The former is more intuitive, and a typical control design process involves varying the relative weights between trajectory errors and control costs until a satisfactory solution is obtained. Following guidelines can be used to choose satisfactory values of $ Q $ and $ R $. ‘norm’ is some measure of magnitude of values in the matrix, $ L_2 $ norm ( square root of sum of square of all matrix entries) is a good choice.

For $ norm(R) » norm(Q) $, control cost is penalized heavily, and the resulting controller drives errors to zero slower.
For $ norm(Q) » norm(R) $, trajectory error cost is penalized heavily, and the resulting controller drives errors to zero very quickly.
It is possible to choose $ R $ such that the individual diagonal elements have different values. In such case, the control corresponding to larger diagonal value will be used sparingly.
It is possible to choose $ Q $ such that the individual diagonal elements have different values. In such case, the states corresponding to larger diagonal values will be driven to zero faster.

The optimal control problem can now be formulated as,

$Minimize ~ J (u)$

Subject to,

$\dot{X} = AX + Bu \text{ and }$ $X(0) = X_0 .$

Noting that the hamiltonian is given by,

$H(X,u, \lambda) = \frac{1}{2} \left( X^TQX + u^T R u \right)+ \lambda^T (AX + Bu)$

The optimality conditions now become,

$\dot{\lambda}= - A^T \lambda + Q X,$ $0= B^T \lambda + R u,$ $\dot{X} = AX + Bu .$

with boundary conditions,

$X(0) = X_0 \text{ and}$ $\lambda_f = S X_f$

We expect control to be a function of states, therefore, we choose $ \lambda = P X $. Substituting,

$\dot{\lambda } = \dot{P} X + P \dot{X}$

$\dot{\lambda}= - A^T \lambda - Q X,$

and using $ \lambda = PX $ and $ \dot{X} = AX + Bu $ gives

$\dot{P} X + P (AX + Bu) = - A^T PX - Q X.$

Substituting $ u= - R^{-1}B^T \lambda = - R^{-1}B^T PX , $

$\dot{P} X + P (AX - B R^{-1}B^T PX) = - A^T PX - Q X.$

Rearranging,

$\dot{P} X = -PAX - A^T PX + P B R^{-1}B^T PX - Q X.$

Expression above holds for all values of $X $, therefore,

$- \dot{P} = PA + A^T P - P B R^{-1}B^T P + Q X.$

with boundary condition $ P_f = S $. The equation above is called Riccati equation, and solving it gives the optimal solution.

** Note, in this derivation we assumed that the final time is fixed. If the final time is also a parameter that can be varied, then an additonal condition $ \frac{\partial \Phi}{\partial t} + H_f = 0 $ is added. **

clc
close all
clear all 

t_f = 5;
dt = 0.001;
P_f= 100*eye(2);
Q = .0001*eye(2);
R = 1;
A = [0 1;0 0];
B = [0 ;1];
P0 =P_f;



% Vectors

N = t_f/dt+1;


% add t_dis array 
t_dis = linspace( 0, t_f, N );
t_res = linspace(t_f, 0, N );

t_dis = 0:dt:t_f;
t_res = t_f:-dt:0;

P_all_res(:,length(t_res))= P_f(:);
for i = length(t_res):-1:2
    P =reshape(P_all_res(:,i),size(A));
    dPdt = -(A.'*P + P*A - P*B*B.'*P + Q); 
    
    P = P - dt*(dPdt);
    P_all_res(:,i-1)= P(:);
end
P_all_res = P_all_res';


X0=[10;0];
X_eul(:,1) = X0;

for i = 2:length(t_dis)
    P_eul = reshape(P_all_res(i-1,:),size(A));
    U_eul(:,i-1) = -inv(R)*B'*P_eul*X_eul(:,i-1);
    X_eul(:,i) = X_eul(:,i-1) + dt* (A*X_eul(:,i-1) + B*U_eul(:,i-1) );  
end

figure
plot(t_dis(1:end-1),U_eul)
ylabel('control')
xlabel('time')

figure;
plot(t_dis,X_eul)
ylabel('states')
xlabel('time')
legend('Position','Velocity')

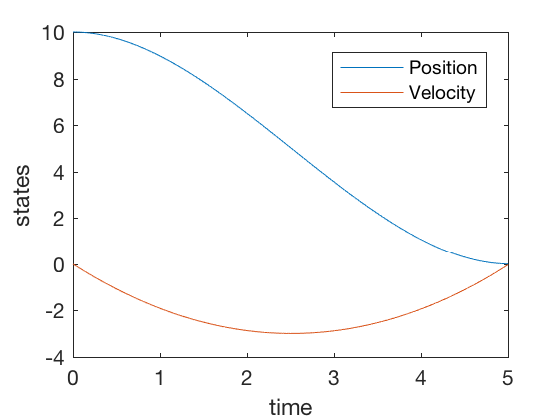
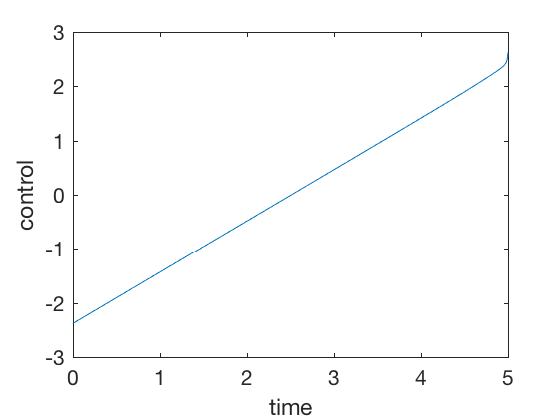
Note the magnitude of control signal is less than 5 units. The strategy is simple, to go down until half point using a linearly increasing control, and then slow down follwing the same linear control shape. None of the PID controls achieve this, further, the required control signals in PID control is of the order of 100s.

Practical considerations

In practice, its better to save the solution of the time-dependent Riccati equation indexed by the time to go. This way, the solution should be computed only once. For example, we can compute the vectors for P backwards for say 100 seconds. So for all controllers that require the states to be minimized within 10 seconds, the appropriate P can be obtained by P corresponding to the time to go. This scheme works only for linear systems because, for linear systems $ \lambda $ is linear in states, which results in Riccati equation that is independent of current states. However, if this were not the case, then the Riccati equation is function of states.

Continuous time infinite horizon, Linear quadratic regulator

The cost function above when time allowed to go to $ \infty $.

$J(u) = \frac{1}{2} \int_{t=0}^{\infty} (X^TQX + u^T R u) dt .$

In steady state condition, $ \dot{P} = 0 $. Therefore, the Riccati equation becomes,

$0 = PA + A^T P - P B R^{-1}B^T P + Q .$

The equation above is algebraic and is a quadratic matrix expression in $ P $. The solution to equation above can be obtained using MATLAB’s ‘care’ function. Example below shows how to use MATLAB’s ‘care’ function to calculate optimal gain values that minimize the cost function above.

K_high = [100 40];
K_low = [40 .8];
x0= [10;0];


M_a = rank(ctrb(A,B));
t = 0:0.01:10;

P = care(A,B,Q,R);
K = inv(R)*B'*P;
K_opt = K
sys_fun = @(t,x)[x(2); -K_opt*x];
[t X_opt] = ode45(sys_fun,t,x0);

K = K_high;
sys_fun = @(t,x)[x(2); -K_high*x];
[t X_high] = ode45(sys_fun,t,x0);

K = K_low;
sys_fun = @(t,x)[x(2); -K_low*x];
[t X_low] = ode45(sys_fun,t,x0);

figure;
plot(t,-K_high*X_high',t,-K_low*X_low',t,-K_opt*X_opt',t_dis(1:end-1),U_eul)
%legend('Control: High K','Control: Low K','Control: Opt K','Position: Fixed time')
figure;
plot(t,X_high(:,1),t,X_low(:,1),t,X_opt(:,1),t_dis,X_eul(1,:))
legend('Position: High K','Position: Low K','Position: Opt K','Position: Fixed time')

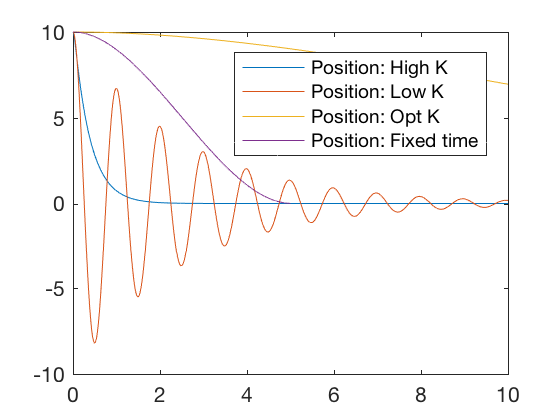
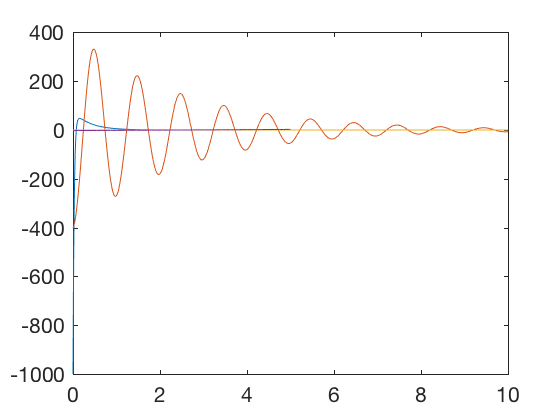
Plots above show that the optimal controller drives errors to zero faster and the required control signal is smaller. Optimal controller can be synthesized for discrete systems also.

Discrete time optimal control

Consider the system dynamic equation given by,

$X[k+1] = f(x[k],u[k])$

with the initial condition $ X[1] = X_0 .$

We aim to find a $ u[k] $ that minimizes,

$J(u) = \Phi(X_f) + \sum_{k=1}^{N} L(X[k],u[k]).$

Following a similar process as we did for continuous time problems, we define a hamiltonian, $ H(X,u,\lambda ) $ as

$H(X[k],u[k],\lambda[k+1] ) = L(X[k],u[k]) + \lambda[k+1]^T f(x[k],u[k])$

The conditions of optimality now become,

$\left. \frac{\partial H}{\partial X} \right|_{X[k],u[k],\lambda[k+1]}^T = \lambda[k]$ $\left. \frac{\partial H}{\partial u} \right|_{X[k],u[k],\lambda[k+1]} = 0$ $\left. \frac{\partial \Phi}{\partial X} \right|_{X_f} = \lambda_f$

Discrete time finite horizon, Linear quadratic regulator

Consider a linear system dynamic equation given by,

$X[k+1] = Ax[k]+ B u[k]$

with the initial condition $ X[1] = X_0 .$

We aim to find a $ u[k] $ that minimizes,

$J(u) =\frac{1}{2} X_f^T S X_f + \frac{1}{2} \sum_{k=1}^{N} \left( X[k]^T Q X[k] + u[k]^T R u[k] \right).$

Following a similar process as above, it can be shown that the necessary conditions for optimality are,

$u[k] = - R^{-1} B^T \lambda [k+1]$ $\lambda[k] = A^T \lambda[k+1] + Q X[k]$ $X[k+1] = Ax[k]+ B u[k]$

With boundary conditions, $ X[1] = X_0 $ and $ \lambda[N+1] = S X_f $.

As the equations are linear in $ X $ and $ u $, we seek a solution of the form

$\lambda [k] = P[k] X[k]$

Using, $ X[k+1] = Ax[k]+ B u[k] $ and $ u[k] = - R^{-1} B^T \lambda[k+1] = - R^{-1} B^T P[k+1] X[k+1] $ in,

$u[k] = - R^{-1} B^T \lambda[k+1]$

gives,

$\lambda[k+1] = P[k+1] X[k+1] = P[k+1] (A X[k] + B u[k]) = P[k+1] (A X[k] - B R^{-1} B^T \lambda[k+1])$ $(I + P[k+1] B R^{-1} B^T)\lambda[k+1] = P[k+1] A X[k]$ $\lambda[k+1] = (I + P[k+1] B R^{-1} B^T)^{-1}P[k+1] A X[k]$

Substituting in costate propogation equation gives

$P[k] X[k] = A^T \left( (I + P[k+1] B R^{-1} B^T)^{-1}P[k+1] A X[k] \right) + Q X[k]$ $P[k] X[k] = A^T (I + P[k+1] B R^{-1} B^T)^{-1}P[k+1] A X[k] + Q X[k]$

As the equation above holds for all $ X[k] $,

$P[k] = A^T (I + P[k+1] B R^{-1} B^T)^{-1}P[k+1] A + Q$

Another form

Discrete time equations can also be obtained in a different form, using

$u[k] = - R^{-1} B^T \lambda[k+1]$ $R u[k] = - B^T P[k+1] X[K+1]$ $R u[k] = - B^T P[k+1] ( A X[k] + B u[k])$ $(R + B^T P[k+1]B ) u[k] = - B^T P[k+1]A X[k]$ $u[k] = - (R + B^T P[k+1]B )^{-1} B^T P[k+1]A X[k]$

The costate equation is,

$\lambda[k] = A^T \lambda[k+1] + Q X[k]$ $\lambda[k] = A^T P[k+1] X[k+1] + Q X[k]$ $\lambda[k] = A^T P[k+1] (A X[k] + B u[k]) + Q X[k]$ $P[k] X[k] = A^T P[k+1] (A - B (R + B^T P[k+1]B )^{-1} B^T P[k+1]A )X[k] + Q X[k]$

Rearranging gives,

$P[k] X[k] = A^T P[k+1] A X[k] - A^T P[k+1] B (R + B^T P[k+1]B )^{-1} B^T P[k+1]A X[k] + Q X[k]$

As this expression holds for all $ X[k] $

$P[k] = A^T P[k+1] A - A^T P[k+1] B (R + B^T P[k+1]B )^{-1} B^T P[k+1]A + Q$

Discrete time infinite horizon, Linear quadratic regulator

Consider a linear system dynamic equation given by,

$X[k+1] = Ax[k]+ B u[k]$

with the initial condition $ X[1] = X_0 .$

We aim to find a $ u[k] $ that minimizes,

$J(u) = \sum_{k=1}^{\infty} \left( X[k]^T Q X[k] + u[k]^T R u[k] \right).$

Under steady state condition or infinite time assumption, $ P[k] = P[k+1] $ and the Riccati equation reduces to

$P = A^T + A^T (I + P B R^{-1} B^T)^{-1}P A + Q$

From the second forumation, the Riccati equation is also written as

$P = A^T P A - A^T P B (R + B^T P B )^{-1} B^T P A + Q$

Note, the two forms of Riccati equations are equivalent, and one follows from another via matrix inversion lemma. Link here provides a very neat proof for matrix inversion lemma. The solution for discrete algebraic Riccati equation can be implemented in MATLAB using ‘dare’ command.

clc
close all
clear all 

t_f = 20;
dt = 0.0001;
t_dis = 0:dt:t_f;
N = length(t_dis);
S{N} = 100*eye(2);
R = dt;
Q = .0001*eye(2)*dt;
A = [1 dt;0 1];
B = [0 ;dt];
K{N} = [0 0];

for i = N-1:-1:1
    %K{i} = inv(R + B'*S{i+1}*B)*B'*S{i+1}*A;
    %S{i} = Q + K{i}'*R*K{i} + (A-B*K{i})'*S{i+1}*(A-B*K{i}); % First form
    %S{i} = Q+ A'*S{i+1}*A - A'*S{i+1}*B*inv(R+B'*R*B)*B'*S{i+1}*A;% Second form    
    S{i} =  A'*inv(eye(2) + S{i+1}*B*inv(R)*B')*S{i+1}*A + Q; % Third form
    K_norm(i) = norm(K{i});
end

X(:,1) = [1;0];
X_dlqr(:,1) = [1;0];
P_dlqr = dare(A,B,Q,R);
K_dlqr = inv(R)*B'*P_dlqr;

for i = 2:N
    u(i-1) = -inv(R)*B'*S{i-1}*X(:,i-1);
    X(:,i) = A * X(:,i-1) + B*u(i-1);
    X_dlqr(:,i) = A * X_dlqr(:,i-1) - B*K_dlqr*X_dlqr(:,i-1) ;

end


figure;
subplot(2,1,1)
plot(t_dis,X(1,:),t_dis,X_dlqr(1,:))
legend('DyP','LQR')
ylabel('position')
subplot(2,1,2)
plot(t_dis,X(2,:),t_dis,X_dlqr(2,:))
legend('DyP','LQR')
ylabel('velocity')
xlabel('time')

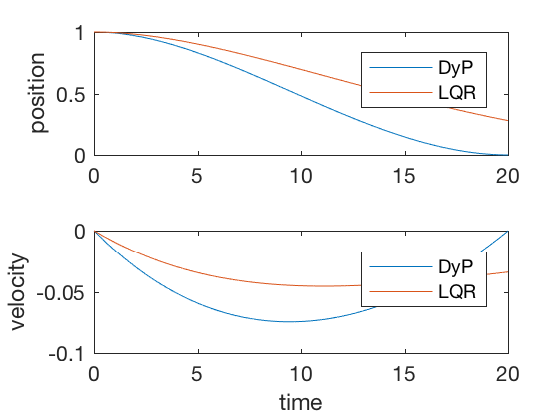
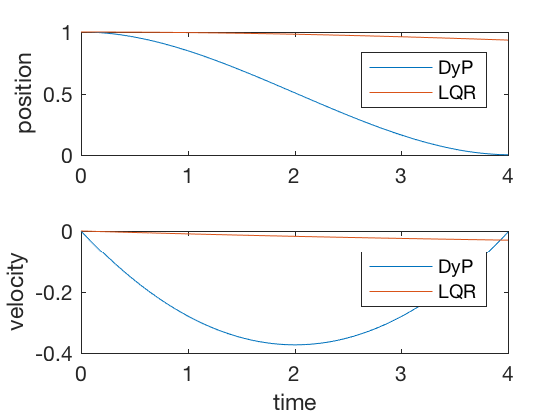
For sufficiently large time to completion, infinite-time solution and finite-time LQR give similar control signals, however, when the final time is kept fixed, the infinite-time approach fails. Figure below present comparison of finite-time and infinite-time outputs for large final time. As can be seen, the controller performances are equivalent in the two cases.

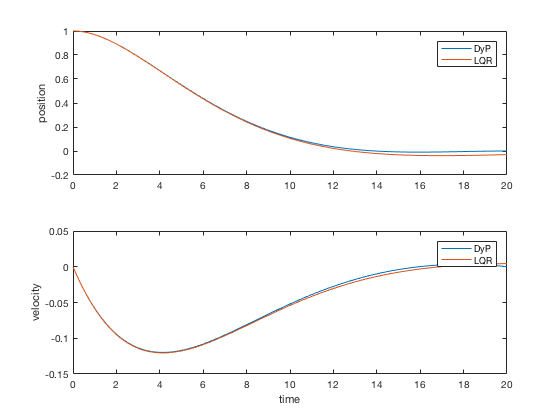
Fig 1. - Finite time vs infinite time LQR solution are equivalent for large time.

** Note: LQR solution using MATLAB’s ‘care’ or ‘dare’ commands are applicable only for infinite time problems. **

Above we derived necessary conditions that an optimal controller has to satisfy. We applied it to discrete and continuous LQR problems and saw one method of computing optimal control to drive errors to zero in a finite time. However, the method above has some limitations,

Not all cost functions can be expressed as LQR problem. Consider the case when we are trying to minimize the time to go.
LQR formulations do not generalize well to conditions when additional constraints are imposed on the system.
- For control inequality constraints, the solution to LQR applies with the resulting control truncated at limit values.
- Dealing with state- or state-control (mixed) constraints is more difficult, and the resulting conditions of optimality are very complex. See Applied optimal control, by Bryson and Ho for detailed treatment.

In the cases above, numerical methods are more suitable.

Dynamic programming

The algebraic equations derived above are very difficult to solve under non-steady state (non-infitite time) assumptions. In such cases, numerical techniques can be used. One such technique is dynamic programming. Dynamic programming is easily applicable to discrete-time problem linear quadratic regulator problem. Dynamic programming is a clever approach to solving certain types of optimization problems, and was developed by Richard Bellman. Its a very versatile method, and can be applied to several different problems. Examples include, path planning, generating shortest cost path between cities, inventory scheduling, optimal control, rondevous problems and many more. The main objective is to compute a cost-to-go function at each state value. Once this cost-to-go map is available, the optimal control policy can be obtained by moving from one state to another state that minimizes the cost to go from that state. A general dynamic programming problem can be represented as,

$J(x[k]) = \underbrace{min}_{u[k]} \left[ L(x[k] , u[k], x[k+1]) + J(x[k+1]) \right]$

In many cases, the expression above is modified as,

$J(x[k]) = \underbrace{min}_{u[k]} \left[ L(x[k] , u[k], x[k+1]) + \gamma J(x[k+1])\right]$

The factor $ \gamma $ discounts the future cost-to-go values. A $ \gamma = 0$ results in an algorithm that completely ignores the future cost-to-go, where as a large $ \gamma $ considers the future rewards more. Having $ \gamma $ is also helpful in numerical methods where we do not know the cost-to-go to start with and estimate it recursively. Having a $ \gamma $ term reduces the contributions of early incorrect assumptions.

Therefore, the task of solving optimal control reduces to finding the cost-to-go function. This can be achieved by solving backwards from the desired state to all the possible initial values. Once this cost-to-go function is known, the optimal control policy reduces to finding the trajectory that minimizes cost from current state to a future state, and cost-to-go from there. Dynamic programming approach is a very generic algorithm and can be applied to optimization problems where cost-to-go and cost of moving from one state to another are additive. Before getting into detailed algroithm development, lets look at a simple example.

Simple example: Dynamic programming

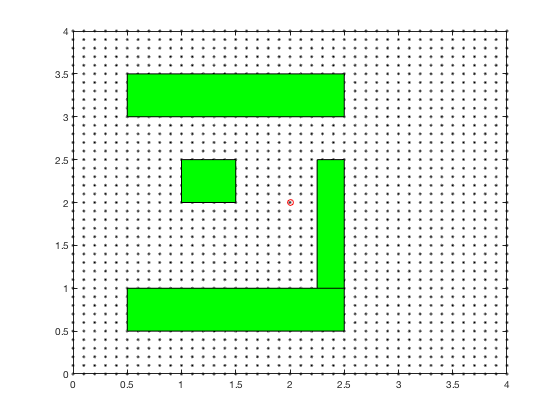
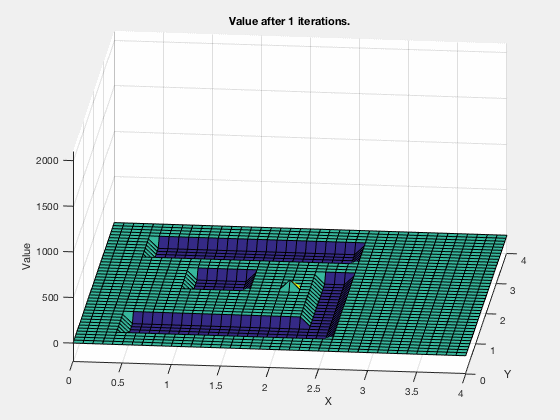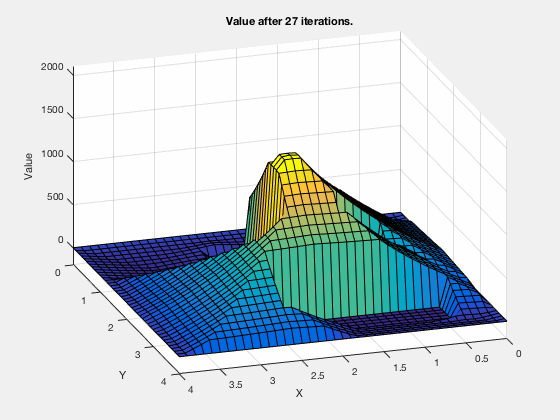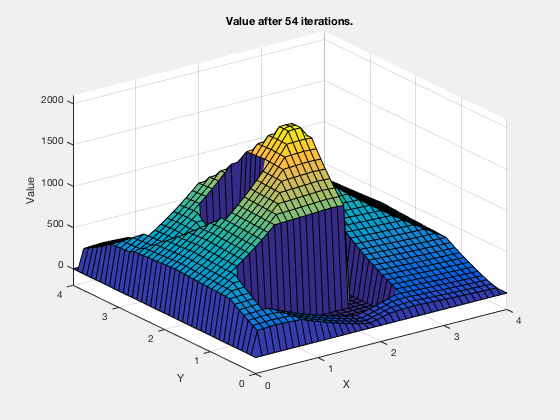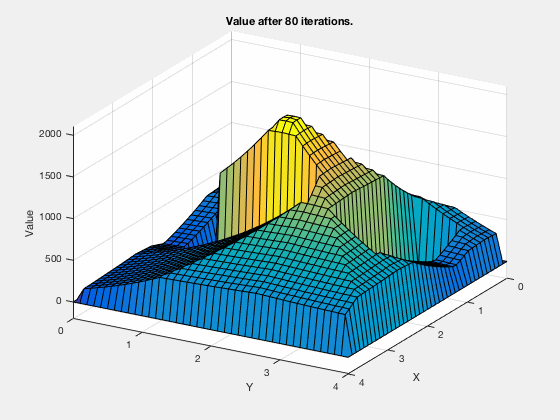
Consider the problem of finding the shortest path between the target and and any start position on the grid in the figure below. We assume that we can move only left, right, up and down, and each action costs us 1 point.

Fig 2. - Dynamic programming set up

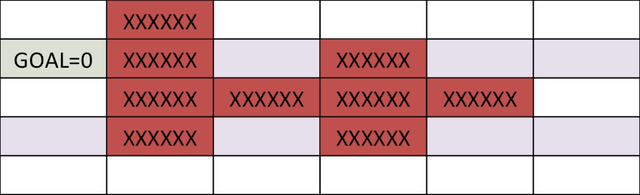
In the example above, its difficult to compute optimal path starting from an initial condition. However, it is much easier to compute cost-to-go if we start from the goal, and step backwards. After the first step, the cells above and below goal have a cost-to-go of 1.

Fig 3. - Cost-to-go after 1 step back

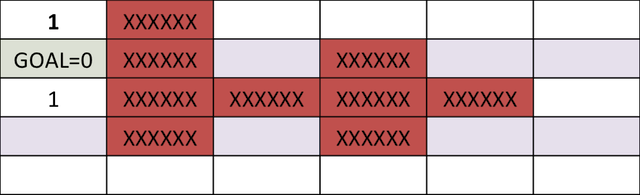
We can carry on this step for next 4 cycles, at which time, the cost-to-go associated with each cell looks as follows. Note, the cells above and to the right of cell corresponding to 5-points both have a score of 6.

Fig 4. - Cost-to-go after 2 steps back

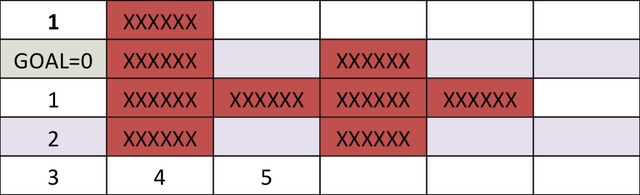
The cost-to-go map for target location is,

Fig 5. - Cost-to-go after 3 step back

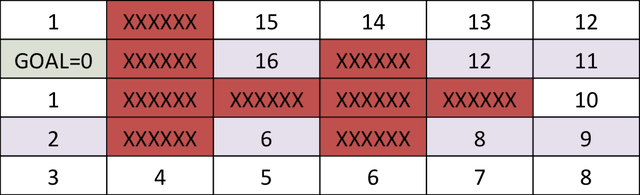
Once we have the cost-to-go for the grid-goal configuration, we can start at any point on the grid and reach the goal by following the path that minimizes the sum of action (1) and cost-to-go. The algorithm performed above is dynamic programming.

Pseudocode to programmatically implement dyanamic programming is as follows,

Initialization
- Set cost-to-go, J to a large value.
- Discretize state-action pairs
- Set cost-to-go as 0 for the goal.
- Set point_to_check_array to contain goal.
Repeat until elements in point_to_check_array = 0
- For point element in point_to_check_array
  - Step backwards from point, and compute cost of taking action to move to the point as cost-to-go from point plus the action cost.
  - If current cost-to-go, J is larger than the cost-to-go from point to moved state, then update cost-to-go for the moved state.
  - Add moved state to a new point_to_check_array

In practice, the algorithm above is difficult to implement, a simpler but computationally more expensive algorithm is as follows,

Initialization
- Set cost-to-go, J to a large value.
- Discretize state-action pairs
- Set cost-to-go as 0 for the goal.
- Set point_to_check_array to contain goal.
Repeat until no-values are updated,
- For each element in the grid, take all the possible actions and compute the incurred costs.
- For each action, compute the cost-to-go of the new state.
- Update self if cost-to-go of the new state plus action is lower than current cost-to-go.

Below is result of applying the algorithm above to

Dynamic programming: Path-planning

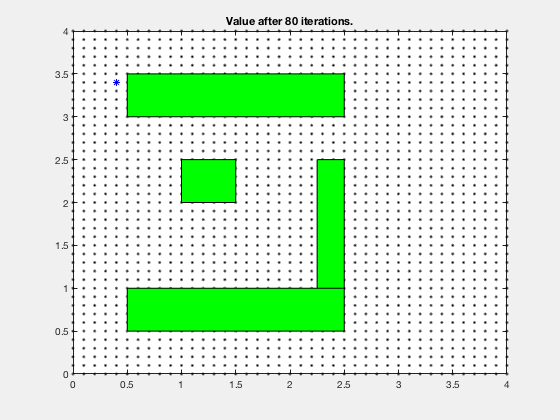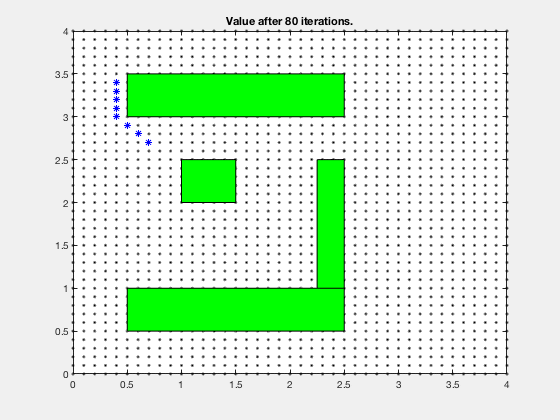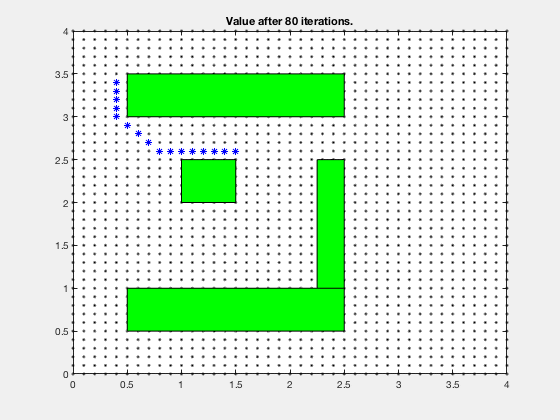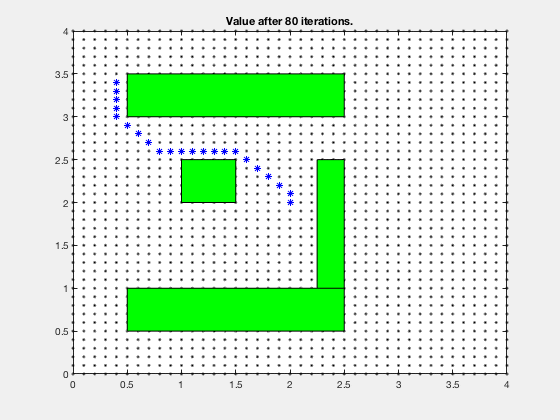
Consider the task of obtaining the shortest path between a desired and final position, given the configuration of obstacles in the environment. We can apply a similar technique as above.

Fig 6. - Cost-to-go after 3 step back

The cost-to-go evolves as shown in the animation below. As can be seen, all the regions corresponding to the obstacles are very high values, and regions closer to the target have lower values.

Fig 7. - Cost-to-go after 3 step back

Fig 8. - Cost-to-go after 3 step back

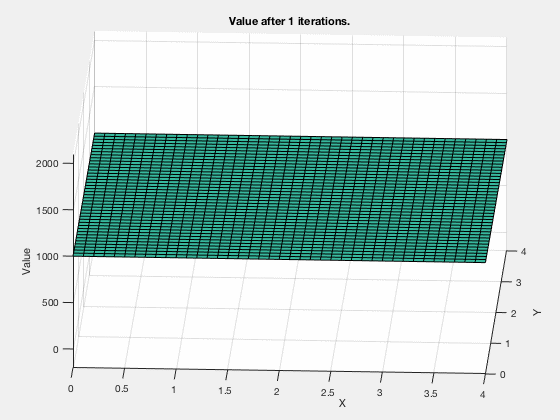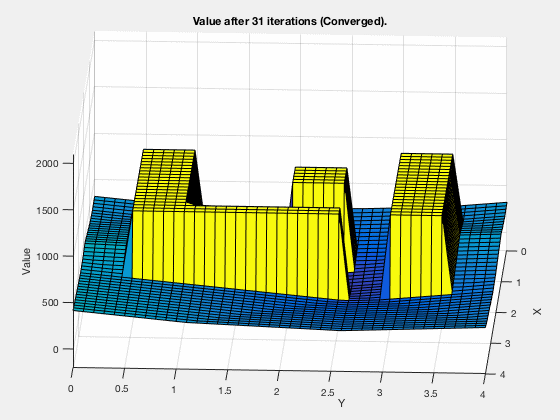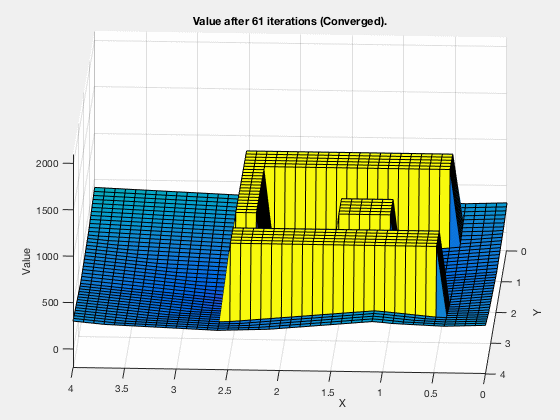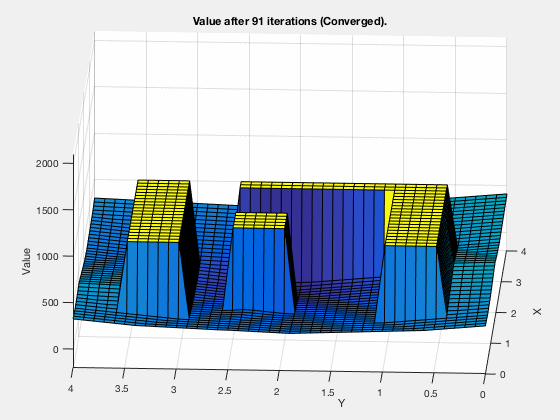
Dynamic programming in control vs reinforcement learning.

The same ideas of dynamic programming can be applied in reinforcement learning also. However, in reinforcement learning the objective is to maximize reward, and in control theory objective is to minimize cost. Below is algorithm for using reinforcement learning that maximizes the reward.

Fig 9. - Cost-to-go after 3 step back

Fig 10. - Cost-to-go after 3 step back

Dynamic programming for linear quadratic regulator control

We will next apply the procedure above to compute optimal control for a linear system given by,

$X[k] = A X[k-1] + B u[k-1]$

Consider designing a controller for the

$J(x[k]) = \underbrace{min}_{u[k]} \left[ \frac{1}{2}\left( X[k]^TQX[k] +u[k]^TRu[k] \right) + J(x[k+1]) \right]$

with

$J(x[N]) = \frac{1}{2} X[N]^T S_NX[N] ,$

being the cost at the end of the cycle. We start the dynamic programming by stepping backwards from $ N $

$J(x[N-1] ) = \underbrace{min}_{u[N-1]} \left[ \frac{1}{2}\left( X[N-1]^TQX[N-1] +u[N-1]^TRu[N-1] \right) + J(x[N] ) \right]$

As $J(x[N] ) = \frac{1}{2} X[N]^TS_NX[N] ,$

$J(x[N] ]) = \frac{1}{2} \left( A X[N-1] + Bu[N-1] \right)^TS_N(A X[N-1] + Bu[N-1]) ,$

Therefore,

$J(x[N-1] ) = \underbrace{min}_{u[N-1]} \left[ \frac{1}{2}\left( X[N-1]^TQX[N-1] +u[N-1]^TRu[N-1] \right) + \frac{1}{2} (A X[N-1] + Bu[N-1])^TS_N(A X[N-1] + Bu[N-1]) \right]$

Note that $ x[N-1] $ does not depend on $ u[N-1] $, therefore, optimal cost-to-go can be computed by taking derivatives with respect to $ u[N-1] $, using matrix derivatives,

$\frac{\partial J(x[N-1] )}{\partial u[N-1]} = \left[ u[N-1]^T R + (A X[N-1] + Bu[N-1])^T S_N B \right] = 0$

As $ R $ and $ S_N $ are symmetric,

$R u[N-1] + B^T S_N (A X[N-1] + Bu[N-1]) = 0$ $u[N-1] = - (R+ B^T S_N B)^{-1} B^T S_N A X[N-1]$

We can rewrite the control above as $ u[N-1] = - K_{N-1} X[N-1] $ where,

$K_{N-1} = (R+ B^T S_N B)^{-1} B^T S_N A X[N-1]$

The cost function $ J(x[N-1]) $ can now be written as,

$J(x[N-1] ) = \left[ \frac{1}{2}\left( X[N-1]^TQX[N-1] +u[N-1]^TRu[N-1] \right) + J(x[N] ) \right]$ $J(x[N-1] ) =\frac{1}{2} \left[ \left( X[N-1]^TQX[N-1] +X[N-1]^T K_{N-1}^T R K_{N-1} u[N-1] \right) + X[N-1]^T(A - B K_{N-1} )^TS_N(A - B K_{N-1} X[N-1] ) \right]$

If we write $ J(x[N-1] ) $ as $ \frac{1}{2} X[N-1]^T S_{N-1} X[N-1]$, then

$S_{N-1} = Q+ K_{N-1}^T R K_{N-1} + (A - B K_{N-1} )^TS_N(A - B K_{N-1})$

The expression above is the Riccati equation we got before with $ S $ substituted for $ P $. The cost-to-go expression between $ ( N-2) $ and $ ( N-1) $ is now,

$J(x[N-2] ) = \frac{1}{2} \underbrace{min}_{u[N-2]} \left[ \left( X[N-2]^TQX[N-2] +u[N-2]^TRu[N-2] \right) + J(x[N-1] \right]$

with

$J(x[N-1] ) = \frac{1}{2} X[N-1]^T S_{N-1} X[N-1] ,$

Dynamic programming for continuous systems involves discretizing the cost-to-go by computing cost between one interval and next as the integral of the cost of control (integrand).

Dynamic programming: LQR example

Consider the system given by $ \ddot{x} = u $, we wish to find a control that minimizes

$J = \frac{1}{2}\int_{u=0}^1 u^2 dt$

with the final state condition to minimize,

$J_f =\frac{1}{2}(10 x^2 + 10 \dot{x}^2)$

We convert this task into dynamic programming task by discetizing the system as,

$\frac{d}{dt} \left [ \begin{array}{c} x_1 \\ x_2 \end{array} \right] =\left [ \begin{array}{cc} 1 & dt \\ 0 & 1 \end{array} \right] \left [ \begin{array}{c} x_1 \\ x_2 \end{array} \right] + \left [ \begin{array}{c} 0 \\ dt \end{array} \right] u$

Corresponding parameters for cost-to-go now become, $ S_N = 10I$, $ Q = 0 $ and $ R = dt $. We will use the equations below to recursively calculate $ S_N s $ and then integrate states forward to compute the optimal control. In practice, $ Q = 0 $ gives numerically unstable results, so we use $ Q = 0.001 dt I $.

$K_{N-1} = (R+ B^T S_N B)^{-1} B^T S_N A X[N-1]$ $S_{N-1} = Q+ K_{N-1}^T R K_{N-1} + (A - B K_{N-1} )^TS_N(A - B K_{N-1})$

clc
close all
clear all 

t_f = 4;
dt = 0.02;
t_dis = 0:dt:t_f;
N = length(t_dis);
S{N} = 100*eye(2);
R = dt;
Q = .0001*eye(2)*dt;
A = [1 dt;0 1];
B = [0 ;dt];
K{N} = [0 0];
K_norm(N)=0;

for i = N-1:-1:1
    K{i} = inv(R + B'*S{i+1}*B)*B'*S{i+1}*A;
    S{i} = Q + K{i}'*R*K{i} + (A-B*K{i})'*S{i+1}*(A-B*K{i});
    K_norm(i) = norm(K{i});
end

X(:,1) = [1;0];
X_dlqr(:,1) = [1;0];
P_dlqr = dare(A,B,Q,R);
K_dlqr = inv(R)*B'*P_dlqr;

for i = 1:N-1
    u(i) = -K{i}*X(:,i);
    X(:,i+1) = A * X(:,i) + B*u(i);
    X_dlqr(:,i+1) = A * X_dlqr(:,i) - B*K_dlqr*X_dlqr(:,i) ;

end

figure;
subplot(2,1,1)
plot(t_dis,X(1,:),t_dis,X_dlqr(1,:))
legend('DyP','LQR')
ylabel('position')
subplot(2,1,2)
plot(t_dis,X(2,:),t_dis,X_dlqr(2,:))
legend('DyP','LQR')
ylabel('velocity')
xlabel('time')

** Note: Hamilton Jacobi Bellman equation is the continuous-time analog of dynamic programming for discrete systems. The conditions for optimality can be obtained using this equation too. **

Numerical methods for optimal control: Shooting methods

In most control applications, there are many constraints, such as actuators cannot apply infinite control, actuators dynamics, the physical limits on states of the system, and further as control designers we could decide to introduce additional contraints. The optimization criteria can be expressed as,

Problem formulation, optimal control with constraints

Find control sequence to minimize,

$J(u) = \Phi(X_f) + \int_{t=0}^{t_f} L(t,X,u) dt .$

Subject to,

$\dot{X} =f(x,u),$

with initial condition $ X(0) = X_0 $, under constraints,

$u_{min} \leq u \leq u_{max},$ $X_{min} \leq X \leq X_{max},$ $C_{eq}(X,u) = 0 ,$ $C(X,u) \leq 0 ,$

where $ C_{eq} $ and $ C $ are equality and inequality constraints on state and control variables.

For control inequality constraints, the solution to LQR applies with the resulting control truncated at limit values. However, dealing with state- or state-control (mixed) constraints is more difficult, and the resulting conditions of optimality are very complex. Several numerical techniques have been developed to design optimal control for such problems. We will try to solve this problem using numerical methods. In particular, we will work with one set of methods called multiple shooting and direct collocation.

There is also a set of indirect collocation methods, where we derive the necessary conditions for optimal control, and make sure the polynomial approximations satisfy the necessary conditions for optimality at the collocation points. This method is typically more accruate, but is not generalizable to different types of problems, because the necessary conditions are very problem specific.

Shooting methods

Conditions of optimality are defined as two point boundary value problems where the states are defined in the initial condition, and costate variables are defined in the final position. Typical solution process involves guessing some value of control sequences to start with, integrating the states fowrard, applying the final state constraints and integrating the costate and state equation backwards. The resulting initial value is compared to the starting initial value, and the control sequence is updated to reduce this error. This process is called single shooting. Shooting comes from the idea of integrating the states forward using a numerical technique, such as euler integration or runge-kutta 4 integration. Integrating forward and backward usually results in large errors because any errors in control policy’s assumptions propogates through out the system. One way to avoid these errors is to use multiple shooting where we discretize the entire trajectory into smaller grids, and we assume the control and state policies in each interval to be polynomials. These points are called knot points. As the control and state variables are arbitary polynomials, they do not satisfy the dynamic equations. Therefore, dynamic equations are introduced as constraints at some intermediate points. In most methods, we choose these points and knot points as the same. However, this results in more variables to be optimized. Further, if we have information regarding control variables, say for example, we expect control to be a cubic function, we can utilize this information to inform our optimizer. Example below illustrates the idea of multiple shooting.

Fig 11. - Progression of states in multiple shooting method.

Parametarization of optimial control using polynomial functions

Express states and control as a piece-wise continuous function of time,

$q_{i,i+1}(t) = p_q(t)$ $u_{i,i+1}(t) = p_u(t)$

The control is parametrized by knot points, $ u_i $ and $ q_i $ for $ i $ going from $ 1 to N+1 $.

Find control sequence to minimize,

$J \left( i: 1 \rightarrow N, u_{i,i+1},q_{i,i+1}) \right) = \Phi_p(q_f) + \sum_{i=1}^N L_p(u_{i,i+1},q_{i,i+1}) .$

Subject to,

$q_{i+1} = \int_{t=t_i}^{t_{i+1}}f(x,u)dt,$

with initial condition

$X(i) = q_i ,$

with control

$u_{i,i+1}(t)$

under constraints,

$u_{min} \leq u_i \leq u_{max},$ $X_{min} \leq q_i \leq X_{max},$ $C_{p,eq}(q_i,u_i) = 0 ,$ $C_p(q_i,u_i)\leq 0 ,$

The cost function above is now a parameter optimization problem in knot points. Nonlinear programming techniques can be used to solve such problems. Numerical optimization methods are approximate methods, and involve a lot of ‘fine-tuning’. This process is best illustrated by an example.

Nonlinear programming: quick review

As state above, we convert optimal control problem into a simpler task of identifying the knot-points, coefficient of polynomials or other parameters that define a state/control trajectory. This is a parameter optimization problem, and is much simpler than solving LQR equations. Say we want to minimize $ f(X) $, such that,

$A X \leq B , \text{ inequality constraint}$ $A_{eq} X = B_{eq} , \text{ equality constraint}$ $C X \leq 0 , \text{ inequality non-linear constraint}$ $C_{eq} X = B , \text{ equality non-linear constraint}$ $X_l \leq X \leq X_u. \text{Bounds}$

Such problems can be solved using nonlinear solvers, such as fmincon.

Fmincon: example 1

$J(X_1,X_2) = 100(X_2^2 -X_1)^2 + (1-X_1)^2$

Subject to the constraint that,

$2X_1+X_2 = 1$

fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

x0 = [0.5,0];
A = [1,2];
b = 1;
Aeq = [2,1];
beq = 1;
x = fmincon(fun,x0,A,b,Aeq,beq)

    0.4149    0.1701

Fmincon: Canon example

Consider the example of firing a cannon such that the cannonball reaches a particular target while requiring minimum firing energy. The equations of motion describing the movement of cannon ball are given by,

$x(t) = v_x t$ $y(t) = v_y t - \frac{1}{2}gt^2$

The objective of optimization is given by,

$\underbrace{Minimize}_{v_x,v_y} (v_x^2+v_y^2)$

The boundary conditions are given by,

$x(t_f) = 10, y(t_f) = 0$ $t_f \geq 0.001$ $v_x \geq 0$ $v_y \geq 0$ $x(t_f) = 10$ $y(t_f) = 10$

clc
close all
clear all


N_grid = 10;

t_f =3;
v_x  = 4;
v_y = 10;

X0 = [t_f;v_x;v_y];

X_opt = fmincon(@(X)cost_fun_cannon(X),X0,[],[],[],[],[],[],@(X)cons_fun_cannon(X),options);


%%% Constraint function 
function [C,Ceq] = cons_fun_cannon(X)
N_grid = (length(X)-3)/3;
t_f = X(1);
vx = X(2);
vy = X(3);
d_x = t_f*vx;
d_y = vy*t_f -1/2*9.8*t_f^2;

C = [-t_f+0.001;
    -vx;
    -vy];
Ceq = [d_y-10;
            d_x - 10;
];

%%% Cost function
function cost= cost_fun_cannon(X)
N_grid = (length(X)-3)/3;
% Cost fun
t_f = X(1);
vx = X(2);
vy = X(3);

cost = vx^2+vy^2;

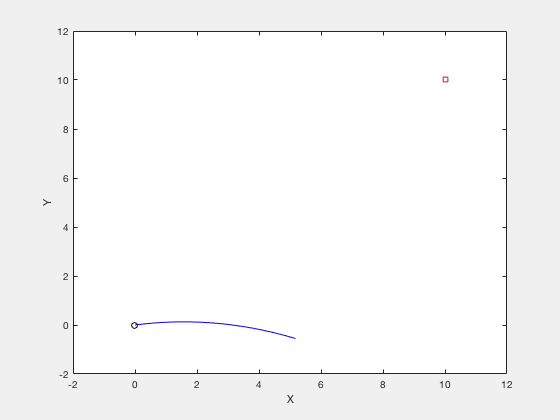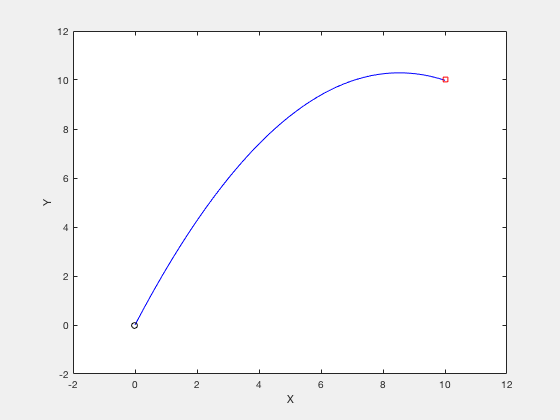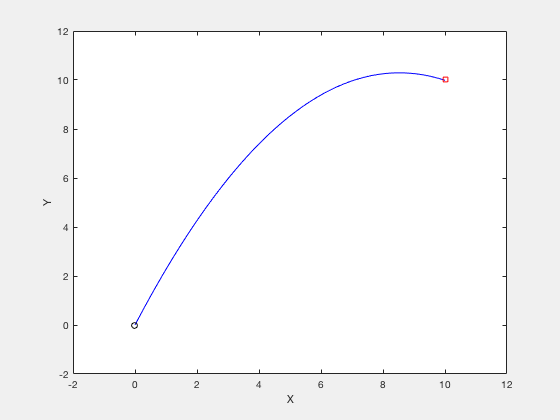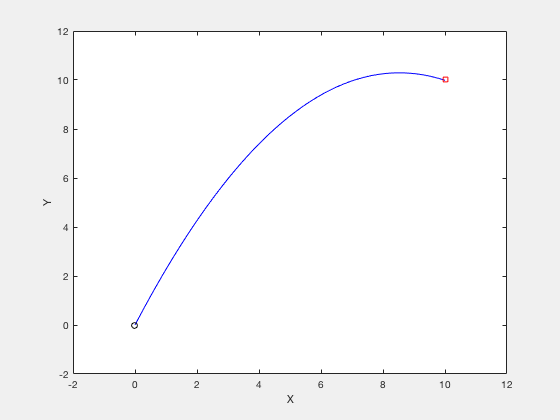
Fig 12. - Cannon optimal shooting problem.

Bang-bang control

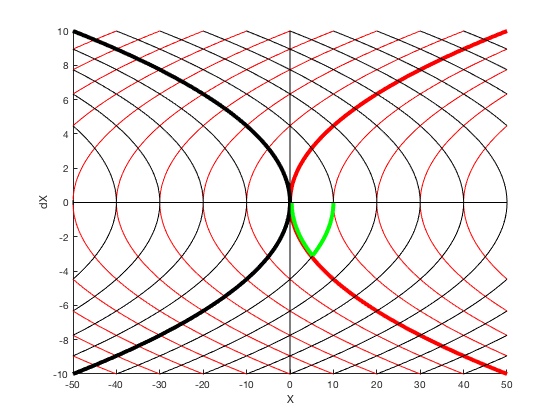
Lets consider the a example of designing control for a double integrator whose control can vary between -1 and 1. If we want to reach from some starting point say 0 to 10, the fastest control solution is to apply 1 control for half the time, and then apply -1. This control can also be indicated by a phase-plot between position and velocity. The red lines indicate trajectory for the case when control is 1, and black lines indicate trajectories when control is -1. The states move on contour lines in clockwise directions. The least-time cost for a particle starting at 0 to go to 10 is given by the green line.

Fig 13. - Minimum time control for double integrator.

Problem formulation,

Given the double integrator system $ \ddot{X} = u $,

$minimize (t_f)$

given,

$-1 \leq u \leq 1$ $X_0 = 0, X_f = 10.$

Solution

We describe control as a piece-wise constant function, and the position and velocity variables defined at the knot points form the additional input to the optimizer. We then integrate the states starting with one knot point to another assuming this control and apply equality constraints between this and the next point. The code snippet below shows this. Complete MATLAB code different examples can be found here.

function [C,Ceq] = cons_fun_doubleIntegrator(X,type)
% Assuming cosntant U
N_grid = (length(X)-1)/3;
% Cost fun
t_f = X(1);
X1 = X(2:N_grid+1);
X2 = X(2+N_grid:2*N_grid+1);
u = X(2+2*N_grid:3*N_grid+1);
C = [];
Ceq = [X2(1) - 0;
    X2(end) + 0;
    X1(1);
    X1(end)-10;
    ];
time_points = (0:1/(N_grid-1):1)*t_f;
for i = 1:(N_grid-1)
    X_0(1,:) = X1(i);    X_0(2,:) = X2(i);
    t_start = time_points(i);t_end = time_points(i+1);
    
    tt = t_start:(t_end-t_start)/10:t_end;
    
    [t,sol_int] = ode45(@(t,y)sys_dyn_doubleIntegrator(t,y,X,type),tt,X_0);
    X_end = sol_int(end,:);
    
    Ceq = [Ceq;
        X_end(1) - X1(i+1);
        X_end(2) - X2(i+1)]; % IMPOSING DYNAMIC CONSTRAINTS AT BOUNDARIES. 
end

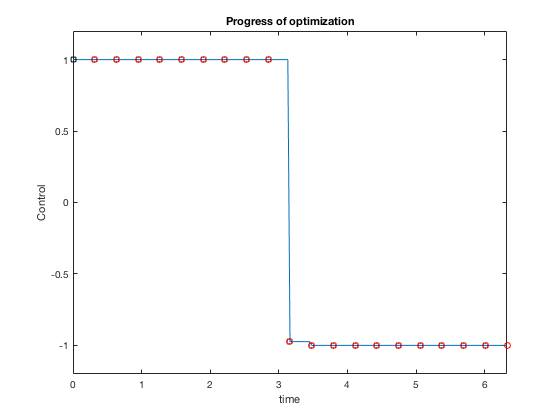
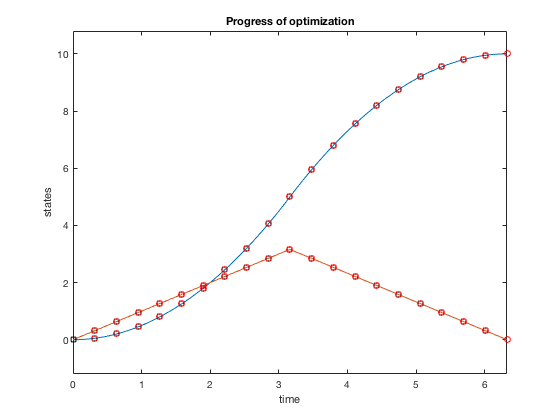
Fig 14. - Minimum time control for double integrator.

Fig 15. - Minimum time states for double integrator.

Plots above present results from optimization. The optimal control strategy that minimizes time of movement while obeying control constraints is one where you accelerate using maximum control, and decelerate using maximum control.

Bang-bang control: Example 2

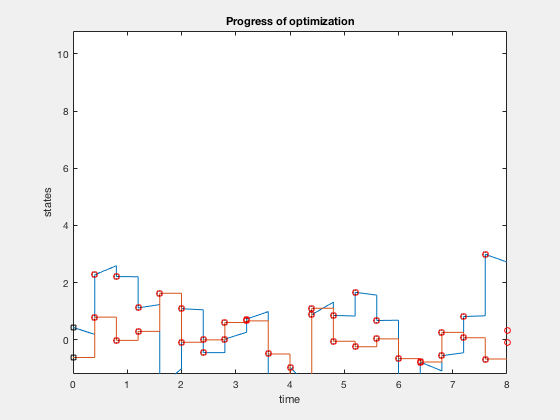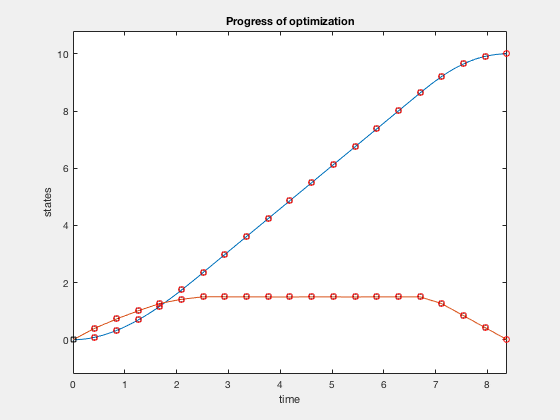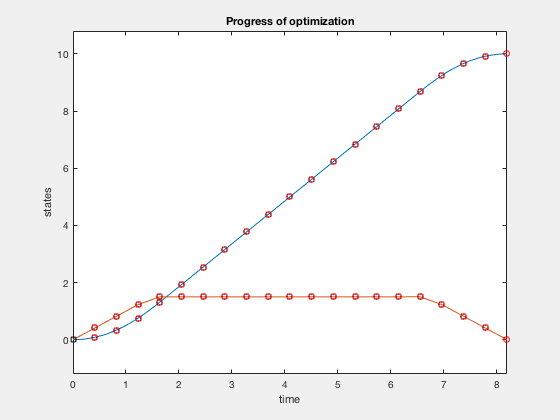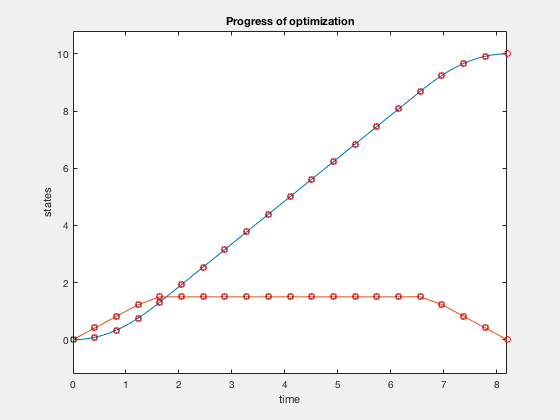
Now we impose additional constraint that the velocity cannot go above 1.5. The problem changes as, given the double integrator system $ \ddot{X} = u $,

$minimize (t_f)$

given,

$-1 \leq u \leq 1$ $\dot{X} \leq 1.5$ $X_0 = 10, X_f = 0.$

Adding additional constraints in Multiple shooting framework is easy. We express the optimization problem as before, however, add additional constraint, that velocity at knot points must be less than 1.5. This can be incorporated by adding just 1 line of code.

function [C,Ceq] = cons_fun_doubleIntegrator(X,type)
% Assuming cosntant U
N_grid = (length(X)-1)/3;
% Cost fun
t_f = X(1);
X1 = X(2:N_grid+1);
X2 = X(2+N_grid:2*N_grid+1);
u = X(2+2*N_grid:3*N_grid+1);
C = [];

function [C,Ceq] = cons_fun_doubleIntegrator(X,type)
% Assuming cosntant U
N_grid = (length(X)-1)/3;
% Cost fun
t_f = X(1);
X1 = X(2:N_grid+1);
X2 = X(2+N_grid:2*N_grid+1);
u = X(2+2*N_grid:3*N_grid+1);
C = [X2-1.5]; % IMPOSING VELOCITY CONSTRAINT. 
Ceq = [X2(1) - 0;
    X2(end) + 0;
    X1(1);
    X1(end)-10;
    ];
time_points = (0:1/(N_grid-1):1)*t_f;
for i = 1:(N_grid-1)
    X_0(1,:) = X1(i);    X_0(2,:) = X2(i);
    t_start = time_points(i);t_end = time_points(i+1);
    
    tt = t_start:(t_end-t_start)/10:t_end;
    
    [t,sol_int] = ode45(@(t,y)sys_dyn_doubleIntegrator(t,y,X,type),tt,X_0);
    X_end = sol_int(end,:);
    
    Ceq = [Ceq;
        X_end(1) - X1(i+1);
        X_end(2) - X2(i+1)]; % IMPOSING DYNAMIC CONSTRAINTS AT BOUNDARIES. 
    
end

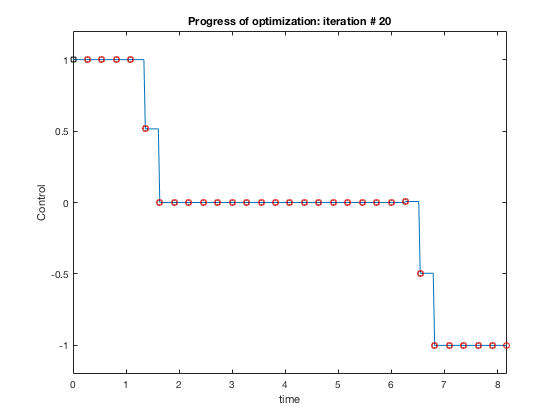
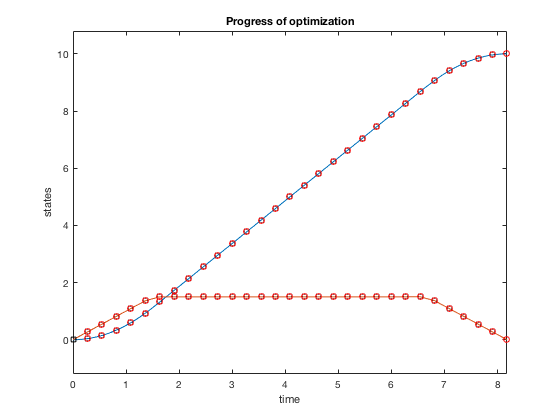
Fig 16. - Minimum time control for double integrator with velocity limit constraint.

Fig 17. - Minimum time states for double integrator with velocity limit constraint.

Plots above show how control policy and states evolve for the the case when velocity is constrained to be less than 1.5. The controller accelerates the particle to the velocity limit using maximum control, then maintains that velocity for some time, and decelerates using maximum decelerating control.

Below are some practical guidelines for desgining optimization routines,

Initialization is very crucial. Its good to initialize states and velocities as linear functions, and control as 0.
The resulting control policy satisfies constraints and dynamic equations only at the knot points. Therefore, to ensure safety have a safety margin within the limits, so intermediate points do not violate boundary constraints.
In cases where you know the form of control equation (polynomial, piecewise constant), use it to inform the optimizer.
Optimality (lowest cost solution) can be improved by either changing the number of grid points or order of polynomials. However, systems with more parameters have larger
Start with a simpler low-dimensional polynomial on a coarser grid and use this to inform an optimizer with more parameters.

Conclusion

In this lesson we went over some concepts of optimal control. We saw how to develop optimal control for linear systems, then looked into designing optimal control under state and control constraints using multiple shooting method. Multiple shooting has one disadvantage that we need to define velocity and position both, which results in $2 N_{grid} \times N_{position}$ variables. However, we did not impose any strict conditions on the state variables. If we approximated postion variables by smooth polynomials whose derivatives are equal at knot points, then the velocity variables are derivative of position variables, and one set of dynamic constraints are satisfied. Therefore, only additional constraint left to satisfy is the second order condition relating acceleration to position and velocity variables. This technique is called direct collocation, which we will discuss in the next class.