MEC 560: Advanced control systems

Assignment 1

Due 9/19/2016 at 4:00 pm.

NO LATE SUBMISSIONS ACCEPTED.

Guidelines and tips to reduce effort:

Please submit assignments inclass or electronically as markdown or MATLAB's live editor with all your work documented in it. There are multiple ways you can prepare this document that will significantly reduce your effort. Below are some options listed from highly-recommended to best-avoid.

  1. Ipython notebooks and MATLAB : If you have anaconda/python and MATLAB installed, you can run MATLAB on ipython notebooks. Ipython notebooks provide easy markdown interface which allows you to add images, equations, websites, audio/video files, code and document your findings all in one place. This however requires some knowledge of typesetting latex equations and basics of markdown. All the course notes, slides and the website were made using ipython notebooks. Moreover, python provides easy interfacing with several webtools, sqlite, apache spark, hadoop, etc.
  2. Use MATLAB's live editor : MATLAB has introduced its own version of notebook-like interface starting 2016 onwards. You can run your scripts in their 'live editors', and it lets you add code, equations, images, text etc in one place and publish the document as HTML or PDF. It is still in nascent stage and is a good option if you are patient. It provides
  3. mbooks MATLAB: m-books are word documents that can include text, code, equations etc and allow you to run the code from microsoft word directly. m-books have all the capability of word, so writing big equations etc is not easy.
  4. Word and MATLAB : Last and perhaps the most common option is to use a document editor such as microsoft word to document your work and MATLAB to run the code. This is the worst of the 3 choices above because in this case you cannot run program and document your code in the same place. So when you submit your file, you will end up submitting one set of word documents, and another of MATLAB codes, and significant ammount of time transfering figures, images and code from MATLAB to word, writing equations in word. Please do not write equations using word's equation editor. Its tedious and very slow. Please use latex software (for example latexit) to typeset your equations in latex and import them to word documents.

PS: You can check the markdown code that generated this section of the document by double clicking on it.

Useful links:

Question 0: Computer set up and installations

Choose any of the methods above and generate a test document.

Question 1: Cayley-Hamilton theorem

Cayley-Hamilton theorem states that a matrix satisfies its own equation, this theorem can be applied to analytically evaluate any function of a matrix. Review the notes on Cayley-Hamilton theorem and given

$$A = \left[ \begin{array}{ccc} 0 & 1 & .5 \\ -2 & -3 & 4 \\ 1 & 8 & 2 \end{array} \right],$$

apply Cayley-Hamilton theorem to compute

  1. sin(A)
  2. \(e^{A} \)

Solution 1

ENTER YOUR WORK HERE

In [25]:
%% Starter code: 

clc
close all
clear all

A = [0,1,.5;
    -2,-3,4;
    1,8,2];
[V,D] = eig(A);

P = randn(3);
inv(P);

B = inv(P)*A*P;
[Vb,Db] = eig(B);

D
Db

D =

   -6.5432         0         0
         0   -0.0411         0
         0         0    5.5843


Db =

   -6.5432         0         0
         0    5.5843         0
         0         0   -0.0411

Question 2: SVD for Image compression

As you saw in class SVD can be applied to compress image. Notes here. For this question you will,

  1. Import your favorite image in MATLAB
  2. Apply SVD and compute how many components are needed to represent 90% of variance
  3. Reconstructuct the image using 4,8,16,32, 64 and 128 components.
  4. Based on your work in parts 2 and 3, how will you compress your image? Quantify reduction in image size and loss of accuracy. Is this loss of accuracy acceptable?

Solution 2

ENTER YOUR WORK HERE

Question 3: Positive (semi-)definite matrices

If \( A \) is a matrix whose all elements are real,

  1. Show that \( A A^T \) is positive semi-definite, i.e. eigen values are all greater than or equal to 0.
  2. Positive semi-definite matrices have a nice property that for any vector \(x \), \(x^T A x \geq 0 \). Under what conditions does the equality occur?

In special case where all eigen values are all positive, the matrix \( A \) is called positive definite, and in such cases \(x^T A x > 0 \).

Question 3: Similarity Transforms:

Two square-matrices \(A \) and \(C \) are called similar if there exists an invertible square matrix \( P \) such that,

$$ C = P^{-1} A P .$$

The transformation \( P^{-1} A P \) is also called similarity or conjugation of \(A\). We will encounter this form of equation when we do transformation of variables in a linear system.

  1. Show that \( A \) and \( C\) have same eigen values.
  2. Do \( A \) and \( C\) have the same eigen vectors?
  3. Consider the dynamic system given by \( \dot{x} = Ax + Bu \). Apply a transformation \( P \) such that the transformed variable \( x = P \hat{x} \).
  4. What will happen in the special case where \(P\) is the matrix of eigen vectors? What can you say about the stability and controlability of the tranformed system by looking at the new dynamics equations?
  5. Consider the system given below, and transform it such that \(P\) is the matrix of eigen vectors. Confirm your predictions from part 4.
$$A = \left[ \begin{array}{ccc} 0 & 1 & .5 \\ -2 & -3 & 4 \\ 1 & 8 & 2 \end{array} \right],$$$$B = \left[ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right],$$
In [26]:
%% Starter code: 

clc
close all
clear all

A = [0,1,.5;
    -2,-3,4;
    1,8,2];
[V,D] = eig(A);

B = [0;1;1];

% calculate modified A_hat and B_hat for this sytem.

Question 4: Particle mass

Equations of motion of a simple point mass moving along a straight line are given by \( M \ddot{x} = F \) with measurement of position only. Express the equation in state space form as \( \dot{x} = Ax + Bu \) and \( y = Cx \).

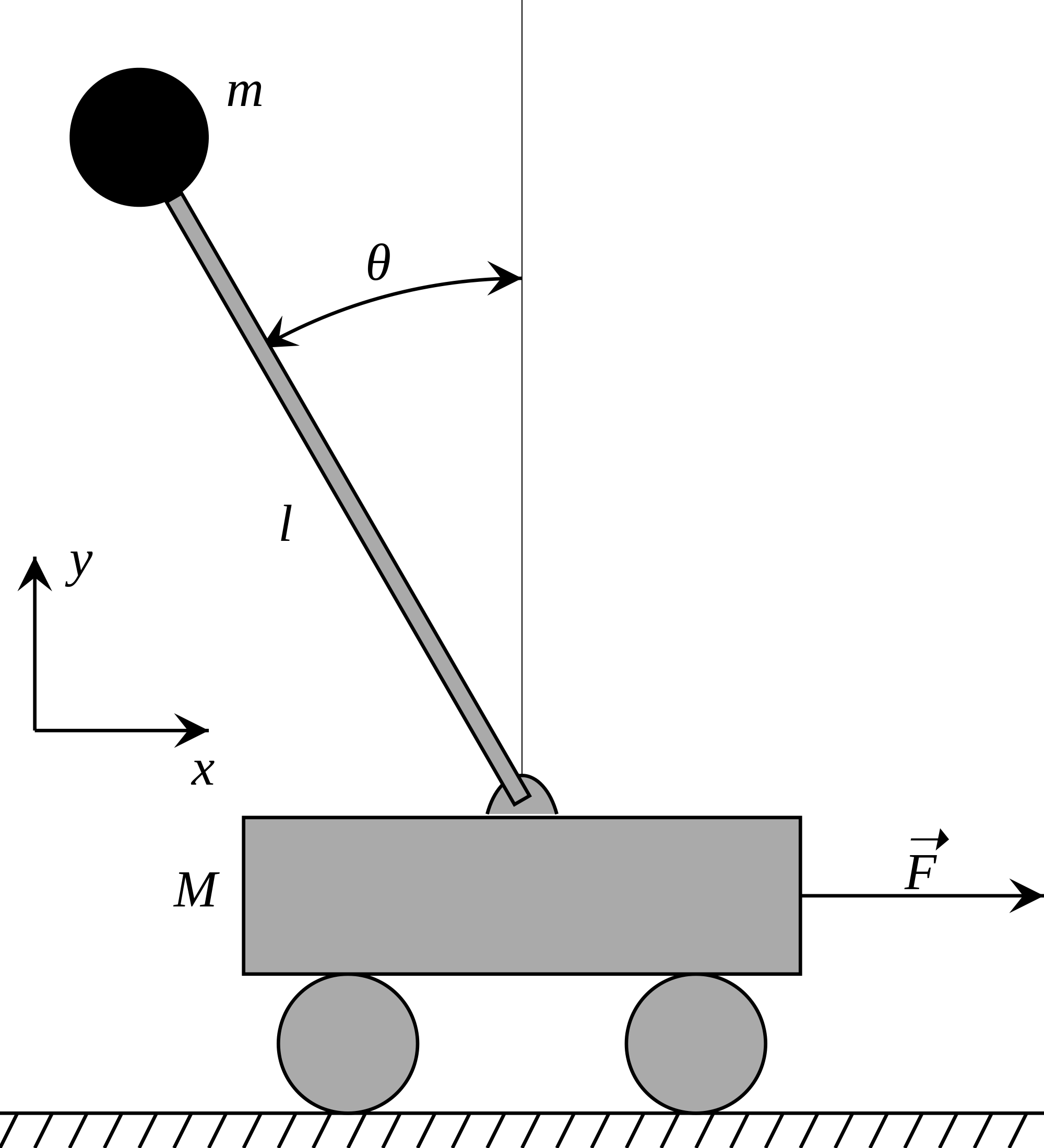
Question 5: Pendulum on a cart example

Derive the equations of motion of a pendulum balancing on a cart, and linearize them about the steady state \( \theta = 0 \) and \( x = 0 \). Express the equations in state space form as \( \dot{x} = Ax + Bu \) and \( y = Cx \).

Question 6: Project idea

By the end of the course you will apply the techniques you learned along the course to a real world problem. Examples include,

  • Humanoid walking
  • Self-parking a car
  • Control of robotic manipulator
  • Driving tractor-trailer in reverse
  • Control of engine dynamics
  • Unmanned aircraft control
  • Control of systems governed by PDEs.

Please answer the following,

  1. I took MEC 560 because (why you took this course).
  2. I am interested in designing a control system for (which type of problem are you interested in? why?).
In [ ]: